Cerința

RAU-Gigel se joacă cu noul său set de cale ferată, primit cadou de ziua lui anul acesta. Setul conține N gări distincte din diverse orașe reprezentative ale României (București, Iași, Sebeș, …), numerotate în continuare, pentru simplitate, cu numere de la 1 la N și N – 1 bucăți de șină care pot conecta între ele câte două gări distincte date (conexiunea este bidirecțională) astfel încât folosind aceste șine există un drum unic alcătuit din șine între oricare două gări distincte. Ca orice jucărie, fiecare din cele N – 1 bucăți de șină are un grad de periculozitate asociat acesteia, o valoare exprimată printr-un număr natural nenul (nimeni nu este perfect până la urmă, nici jucăriile), pentru a ști de la ce vârsta ar fi bine să poată fi folosite de copii, de exemplu. De asemenea, toate bucățile de șină au aceeași lungime constantă, de o unitate.

RAU-Gigel își desfășoară joaca pe parcursul a Q zile și în fiecare zi este supravegheat de câte un membru al familiei pentru a fi în siguranță. Din nefericire pentru el, în fiecare din cele Q zile persoana care îl supraveghează îi încurcă puțin planurile, permițându-i să folosească doar șinele care au gradul de periculozitate cel mult M (inclusiv M), o valoare naturală nenulă aleasă de aceasta (de remarcat că poate mereu folosi toate gările). Astfel, folosind toate șinele pe care le are la dispoziție pentru a conecta între ele gările corespunzătoare, va obține una sau mai multe așezări conexe maximale de gări (există un drum unic alcătuit din șine între oricare două gări distincte dintr-o așezare) pe care le va numi în continuare orașe. În fiecare astfel de zi, personajul nostru principal primește de la persoana care îl supraveghează un număr natural nenul K de bucăți de șină considerate perfect sigure pentru joaca copilului de către respectivul supraveghetor, cu care poate conecta oricare două gări distincte dorește. De asemenea, șinele primite îi sunt luate la finalul zilei (poate că persoana respectivă mai supraveghează și alți copii în următoarele zile și mai are nevoie de ele).

RAU-Gigel consideră că un lanț este un șir de una sau mai multe gări distincte astfel încât oricare două gări adiacente din acesta sunt conectate de exact o șină, iar lanțul de lungime maximă este cel format dintr-un număr maxim de bucăți de șină (astfel, lungimea unui lanț este dată de numărul de bucăți de șină din care este alcătuit). Scopul acestuia este ca în fiecare zi să formeze un singur lanț cât mai lung având la dispoziție șinele primite de la supraveghetor și cel mult câte un lanț din fiecare oraș creat de acesta, la alegere (adică pentru fiecare oraș poate să aleagă exact un lanț din el (oricare dorește) sau să nu folosească niciun lanț din acel oraș).

RAU-Gigel cunoaște deja toate detaliile a T astfel de scenarii de joacă independente și vrea pentru fiecare dintre acestea, pe baza informațiilor date, să-l ajutați să afle în fiecare zi care este lungimea maximă a unui lanț de șine pe care îl poate obține în modul descris anterior (prima cerință), respectiv numărul de modalități distincte de obținere a acestui maxim (a doua cerință), calculat modulo 1.000.000.007. Două modalități de obținere a maximului sunt considerate distincte dacă cele două submulțimi de orașe din care acesta a selectat lanțurile de lungime maximă sunt diferite.

Date de intrare

Fișierul de intrare cfr.in conține pe prima linie un număr natural nenul T, reprezentând numărul de scenarii. Pentru fiecare scenariu pe prima linie se află un număr C care reprezintă numărul cerinței care trebuie rezolvată.

Pe cea de-a doua linie se află N, numărul de gări, urmat de N – 1 linii care reprezintă descrierile șinelor de tren: câte 3 numere u_i v_i w_i pe fiecare linie, care reprezintă gările conectate, respectiv gradul de periculozitate pentru bucata de șină cu numărul i, 1 ≤ i < N.

Pe următoarea linie se află numărul Q urmat de descrierile celor Q zile de joacă: câte 2 numere M_i K_i pe fiecare linie, având semnificațiile din enunț, 1 ≤ i ≤ Q.

Date de ieșire

Fișierul de ieșire cfr.out va conține răspunsurile, în ordinea solicitării, adică lungimea maximă care poate fi obținută în condițiile zilei corespunzătoare dacă C = 1 sau numărul de modalități distincte de a obține această lungime maximă modulo 1.000.000.007, dacă C = 2.

Restricții și precizări

• 1 ≤ T ≤ 3
• 1 ≤ C ≤ 2
• 1 ≤ N, Q ≤ 100.000
• 1 ≤ u_i, v_i ≤ N
• 1 ≤ w_i, M_i ≤ 1.000.000.000
• 1 ≤ K_i ≤ N
• Un lanț poate fi format dintr-o singură gară sau să aibă la cele 2 capete ale sale câte o gară.
• Nu este obligatoriu ca într-o zi să se folosească toate cele K_i șine primite (mai ales că acest lucru s-ar putea să fie imposibil, pentru că o bucată de șină primită trebuie să conecteze exact două gări distincte într-un lanț).
• Pentru teste în valoare de 10 de puncte, C = 1 pentru toate scenariile și 1 ≤ N, Q ≤ 1.000.
• Pentru alte teste în valoare de 10 de puncte, C = 1 pentru toate scenariile și M_i = 1.000.000.000, 1 ≤ i ≤ Q.
• Pentru alte teste în valoare de 10 de puncte, C = 1 pentru toate scenariile și u_i=i, v_i = i+1, 1 ≤ i < N.
• Pentru alte teste în valoare de 10 de puncte, C = 1 pentru toate scenariile și K_i=1, 1 ≤ i ≤ Q.
• Pentru alte teste în valoare de 10 de puncte, C = 1 pentru toate scenariile și nu există restricții suplimentare.
• Pentru alte teste în valoare de 10 de puncte, C = 2 pentru toate scenariile și 1 ≤ N, Q ≤ 1.000.
• Pentru alte teste în valoare de 10 de puncte, C = 2 pentru toate scenariile și M_i=1.000.000.000, 1 ≤ i ≤ Q.
• Pentru alte teste în valoare de 10 de puncte, C = 2 pentru toate scenariile și u_i=i,v_i=i+1, 1 ≤ i < N.
• Pentru alte teste în valoare de 10 de puncte, C = 2 pentru toate scenariile și K_i=1, 1 ≤ i ≤ Q.
• Pentru alte teste în valoare de 10 de puncte, C = 2 pentru toate scenariile și nu există restricții suplimentare.

Exemplul 1:

cfr.in

1
1
13
1 2 1
1 3 2
1 4 2
2 5 3
3 6 1
4 7 3
4 8 2
5 9 4
5 10 4
5 11 4
8 12 3
8 13 1
4
2 10
3 2
1 4
4 3

cfr.out

11
7
7
6

Explicație

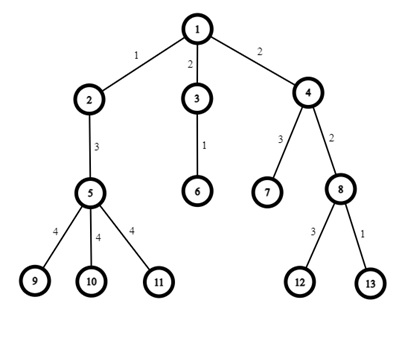
La final se află o reprezentarea vizuală a rețelei de gări, respectiv șine corespunzătoare acestui exemplu (pe șine s-a trecut gradul lor de periculozitate, iar lungimea tuturor este, cum s-a precizat și în enunț, constantă, de o unitate).

Să considerăm prima zi. Avem la dispoziție doar șinele de tren cu grad de periculozitate cel mult 2, așa că așezările de gări formate sunt: {1, 2, 3, 4, 6, 8, 13}, {5}, {7}, {9}, {10}, {11}, {12}, în total 7 așezări. RAU-Gigel poate alege din prima așezare lanțul de gări 6 – 3 – 1 – 4 – 8 – 13, de lungime 5 (șine), iar din restul așezărilor există câte o singură opțiune de alegere, care este mereu un lanț format dintr-un singur nod, de lungime 0 (șine). Observăm că RAU-Gigel are la dispoziție destule șine adiționale primite pentru a “lega” toate lanțurile alese, astfel poate obține lanțul: 6 – 3 – 1 – 4 – 8 – 13 – 5 – 7 – 9 – 10 – 11 – 12, de lungime 11 (șine). Oricum ar alege alte lanțuri, RAU-Gigel nu poate obține un lanț final de lungime strict mai mare, deci răspunsul pentru prima zi este 11. De asemenea, se remarcă faptul că nu s-au folosit toate bucățile de șină primită, ci doar 6 din cele 10. RAU-Gigel nu mai poate folosi șinele rămase pentru a prelungi lanțul obținut (de exemplu să atașeze încă o șină la unul din capetele lanțului, să zicem la 12) pentru că o șină trebuie să unească exact 2 gări distincte.

Exemplul 2:

cfr.in

1 
2
13
1 2 1
1 3 2
1 4 2
2 5 3
3 6 1
4 7 3
4 8 2
5 9 4
5 10 4
5 11 4
8 12 3
8 13 1
4
2 10
3 2
1 4
4 3

cfr.out

1
3
21
1

Explicație

Reprezentarea vizuală a rețelei de gări, respectiv șine corespunzătoare acestui exemplu este identică cu cea a primului exemplu și se găsește la final.

Să considerăm a doua zi. Avem la dispoziție doar șinele de tren cu grad de periculozitate cel mult 3, așa că așezările de gări formate sunt: {1, 2, 3, 4, 5, 6, 7, 8, 12, 13}, {9}, {10}, {11}, în total 4 așezări, pe care le numerotăm de la 1 la 4 în ordinea în care sunt scrise. Se observă că lungimea maximă a unui lanț pe care îl poate obține RAU-Gigel în modul descris în enunț este de 7 șine. De asemenea, se mai observă și că într-o soluție optimă acesta este mereu obligat să aleagă un lanț de lungime 5 din prima așezare (nu contează care din ele chiar dacă există mai multe), iar apoi poate alege oricare 2 “lanțuri” distincte din așezările rămase pentru că toate sunt formate dintr-un singur nod și au lungimea 0 (șine), RAU-Gigel formând astfel un lanț de lungime 7 în urma utilizării celor două șine primite adițional în această zi. Astfel, soluțiile optime sunt: {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, în număr de 3 (de remarcat din nou că “forma” unei soluții este dată de așezările din care s-au ales lanțurile, nu de gările / șinele din care este alcătuit lanțul final).