O matrice pătratică A_{ij} de dimensiuni N x N cu N impar se numește matrice spirală dacă respectă următoarele proprietăți când este parcursă în spirală conform imaginii de mai jos:

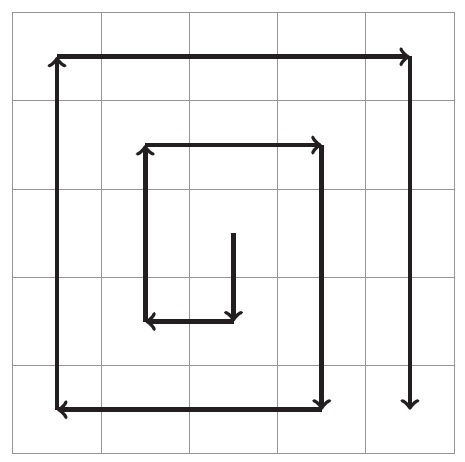
• Pentru oricare celulă (i, j) din matrice, fie A[i, j] = 0, fie A[i,j] nu conține cifra 0.
• Fie (i, j) oricare celulă mai puțin cea din centru și (k, l) celula parcursă anterior din matrice, și fie c oricare cifră nenulă, adică de la 1 la 9:
  a) Dacă c divide i + j, atunci A[i, j] conține cifra c dacă și numai dacă A[k, l] nu conține cifra c.
  b) Dacă c nu divide i + j, atunci A[i, j] conține cifra c dacă și numai dacă A[k, l] conține cifra c.
  c) Pentru numărul aflat în celula din centru, fiind prima parcursă, nu avem astfel de restricții.

• Un element din matrice va fi 0 dacă și numai dacă acesta nu are voie să conțină nicio cifră de la 1 la 9 conform regulilor de mai sus.

Cerința

Dându-se o matrice pătratică A de dimensiune N, trebuie să determinați care este numărul minim de elemente din matrice care ar trebui înlocuite (în celulele respective pot fi scrise orice alte numere naturale) pentru ca A să devină o matrice spirală.

Date de intrare

Pe prima linie a fișierului de intrare spirala.in se va afla un singur număr natural N, reprezentând dimensiunile matricii. Pe următoarele N linii se vor afla câte N numere naturale separate prin câte un spațiu reprezentând elementele matricii A.

Date de ieșire

Fișierul de ieșire spirala.out va conține un singur număr reprezentând minimul de elemente ce vor trebui înlocuite pentru ca A să devină o matrice spirală.

Restricții și precizări

• 1 ≤ N ≤ 999, N impar.
• Elementele matricii A sunt numere naturale mai mici decât 1.000.000.000 ce conțin doar cifre de la 1 la 9, cu excepția elementelor egale cu 0.

Exemplu:

spirala.in

5
16 36 1234 23456 145
26 1469 4569 123459 457
1236 269 13579 234579 12578
346 12569 359 135789 235789
13456 245 12457 578 45789

spirala.out

2

Explicație

Pentru a obține o matrice spirală, ar trebui înlocuite numerele din celulele (1,3) și (5, 5). În celula (1, 3) ar putea fi scris numărul 12345 și în celula (5, 5), numărul 13789.