Cerința

Se dau un arbore cu N noduri și rădăcina în nodul 1 al cărui muchii au lungimi exprimate prin numere naturale nenule și Q query-uri de forma u v. Pentru fiecare query să se afle suma lungimilor tuturor drumurilor distincte de la un nod aflat în subarborele cu rădăcina în nodul u la un nod aflat în subarborele cu rădăcina în nodul v modulo 109 + 7. (lungimea unui drum este egală cu suma lungimilor tuturor muchiilor ce îl alcătuiesc).

Date de intrare

Pe prima linie se vor citi de la tastatură numerele N și Q reprezentând numărul de noduri din arbore, respectiv numărul de query-uri.

Următoarele N - 1 linii conțin câte 2 numere \( {p}_{i}\ {w}_{i} \), \( i = \overline{2,N} \), reprezentând tatăl nodului i în arbore, respectiv lungimea muchiei dintre \( {p}_{i} \) și i(nodul 1 este rădăcina arborelui, deci nu are tată).

Pe următoarele Q linii se va afla câte un query.

Date de ieșire

Programul va afișa pe ecran pe câte o linie rezultatele query-urilor, în ordinea în care acestea apar în input.

Restricții și precizări

• 1 ≤ N ≤ 200.000
• 1 ≤ Q ≤ 500.000
• 1 ≤ wi ≤ 1.000.000.000
• 1 ≤ u, v ≤ N
• pentru fiecare query de tipul 2, subarborii cu rădăcinile în nodurile u, respectiv v nu vor avea noduri comune

Exemplu:

Intrare

14 4
1 4
1 3
2 2
2 7
2 10
3 12
3 5
4 8
4 1
5 3
7 6
7 4
8 9
4 8
2 7
9 11
12 8

Ieșire

129
595
20
55

Explicație

Arborele descris în exemplu arată în felul următor:

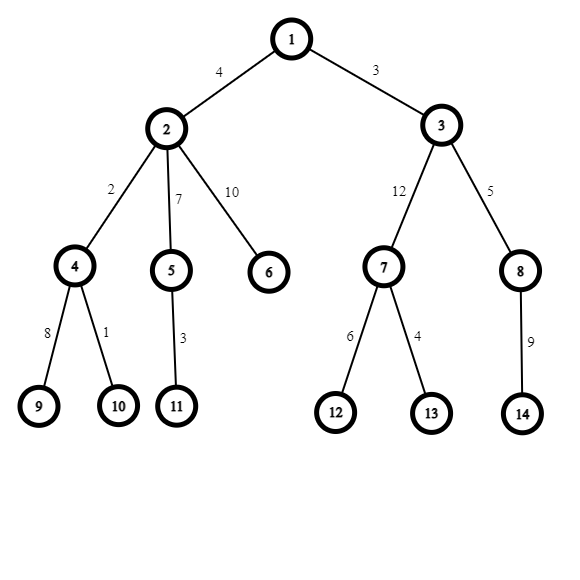
Pentru primul query drumurile sunt:

• De la 4 la 8 de lungime 14
• De la 4 la 14 de lungime 23
• De la 9 la 8 de lungime 22
• De la 9 la 14 de lungime 31
• De la 10 la 8 de lungime 15
• De la 10 la 14 de lungime 24

Total: 14 + 23 + 22 + 31 + 15 + 24 = 129