Lista de probleme 6

Sărbătorile de iarnă tocmai s-au încheiat. Florinel dorește să-și ajute părinții la despodobirea bradului. Tubul luminos pe care l-au folosit anul acesta este mai special. Are N3 becuri luminoase numerotate de la 1 la N3, iar fiecare bec care este inscripționat cu un număr prim, va rămâne mereu aprins. Cutia în care trebuie strâns tubul este un cub de latură N. Becul cu numărul 1, trebuie pus în colțul de coordonate (1,1,1), restul în spirală până la umplerea nivelului, apoi nivelul următor în sens invers, ș.a.m.d.

Cunoscând latura N a cubului, să se umple cubul cu tubul luminos (becurile fiind legate crescător), apoi să se determine:

1. Coordonatele (x,y,z) ale becului cu numărul V. (x-linia, y-coloana, z-înălțimea)
2. Numărul de becuri luminoase situate pe fiecare față a cubului.

Leneşul este un animal foarte leneş. El se deplasează numai în linie dreaptă, dar face din când în când câte un popas. În această problemă leneşul trebuie să traverseze de la nord la sud şi înapoi un teren reprezentat de o matrice de dimensiuni M×N cu valori numere naturale. Valorile reprezintă efortul cerut pentru traversarea zonei respective. Leneşul va alege o coloană pentru traversarea matricei, iar pentru popasuri, în număr de k1, va alege zone alăturate drumului din coloana din stânga sau cea din dreapta. În cazul în care se va întoarce va proceda la fel, dar va face k2 popasuri. Regulile problemei cer ca cele două drumuri să nu aibă zone comune.

Cunoscând dimensiunile M, N ale terenului, numărul de popasuri k1, k2 și efortul pentru traversarea fiecărei zone a terenului, să se determine:

1. Efortul minim de parcurgere a terenului de la Nord la Sud, folosind k1 popasuri.
2. Efortul minim de parcurgere a terenului de la Nord la Sud și înapoi de la Sud la Nord, folosind k1 popasuri la deplasarea Nord – Sud, respectiv k2 popasuri la deplasarea Sud – Nord.

Pentru a participa la un concert, n persoane s-au așezat la coadă pe un singur rând în așteptarea deschiderii casei de bilete. Înălțimile celor n persoane sunt toate distincte. Pe baza acestei informații cruciale, agenții de securitate au decis ca din motive de … securitate, ordinea persoanelor care așteaptă la coadă trebuie schimbată în funcție de înălțimile lor.

Astfel, agentii de pază vor alege, pe rând, câte o persoană și o vor trimite la sfârșitul rândului. După fiecare operație de tipul acesta, să-i spunem “de mutare”, rândul se restrânge, ocupându-se poziția rămasă liberă. Strategia agenților de pază este aceasta: la terminarea tuturor operațiilor de mutare, riscul minim de securitate se obține dacă toate persoanele aflate în dreapta persoanei celei mai înalte vor fi mai înalte decât cele aflate în stânga persoanei cele mai înalte. În plus, înalțimile persoanelor vor fi crescătoare până la poziția k a persoanei celei mai înalte și descrescătoare după poziția k.

Mai exact: dacă h[1], h[2], …, h[n] sunt înălțimile persoanelor după finalizarea operațiilor de mutare, atunci: există o poziție k, cu 1 ≤ k ≤ n astfel încât h[1] < h[2] < ... h[k-1] < h[k] > h[k+1] > … > h[n-1] > h[n] și în plus h[i] < h[j] pentru oricare i < k și k < j.

Deoarece o asemenea logică este greu de combătut, iar agenții nu au aerul că vor să glumească, persoanele care așteaptă la coadă vor accepta toate mutările impuse de către aceștia.

Cunoscând numărul de persoane n și înălțimile h[1], h[2], …, h[n] ale acestora să se scrie un program care determină :

1. Poziția persoanei celei mai înalte în rândul inițial, în cazul în care nu sunt necesare operații de mutare.
2. Numărul minim de mutări necesare pentru ca rândul de persoane să prezinte un risc minim de securitate.

În această poveste este vorba despre o casă cu mai multe camere. O cameră are forma unui pătrat de latură 1. Dacă două camere au un perete comun, atunci se poate trece dintr-o cameră în alta. Casa nu are neapărat formă dreptunghiulară.

O asemenea casă poate fi descrisă în povestea noastră în două moduri:

• prin matricea minimală: o matrice cu elemente 0 şi 1 în care există N valori egale cu 1, ce corespund camerelor, iar prima linie, ultima linie, prima coloană şi ultima coloană au cel puţin un element egal cu 1.
• prin construcţie: un şir de N-1 perechi (a[i], b[i]) 1≤i<n în care a[i] din {1,2,…,i} şi b[i] din {N, S, E, V}. Camerele vor fi numerotate de la 1 la n. Perechea (a[i], b[i]) precizează poziţia camerei i+1 faţă de camera a[i]: E înseamnă la dreapta (est), N deasupra (nord), V la stânga (vest), S dedesubt (sud). Observaţi că pentru prima cameră nu există nicio precizare!

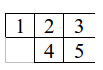
De exemplu, casa de mai sus poate fi descrisă de şirul (1 E) (2 E) (2 S) (3 S), adică a doua cameră e “lipită” la est de prima cameră, următoarea (a treia) la est de camera 2, a patra la sud de camera 2, iar ultima la sud de camera 3.

Cerința

1. Se dă descrierea unei case prin construcţie şi se cere descrierea acesteia prin matricea minimală.
2. Se dă descrierea unei case prin matricea minimală şi se cere descrierea acesteia prin construcţie.

Un arheolog a găsit un sipet interesant. După ce l-a deschis cu grijă, a constatat cu surprindere că sipetul conține bănuți de aur. Uitându-se mai atent a mai găsit ceva: un pergament ascuns într-un compartiment secret al sipetului, cu un text scris într-o limbă antică, pe care, din fericire, arheologul o cunoștea. Din text a reieșit că un grup de negustori foarte bogați a vrut să ascundă în mare secret averea breslei lor, formată din monede de aur, deoarece se prevestea un război cumplit. Negustorii știau că există șanse ca această comoară să fie găsită și confiscată de dușmani, deci s-au sfătuit cum e mai bine să procedeze, cum să ascundă comoara. Arheologul a reușit să deducă din text următoarele:

a) Cele N monede, care formau averea breslei, au fost împărțite în maximum trei feluri de grămezi, formate din p1, p2 și p3 bănuți, p1, p2 și p3 fiind numere prime consecutive, p1<p2<p3. Fiecare grămadă a fost pusă în întregime într-un sipet.
b) Este posibil să existe 0 (zero) grămezi formate din p1 sau p2 sau p3 monede, scopul fiind să se obțină o împărțire în care numărul monedelor rămase nedistribuite să fie minim, iar dacă există mai multe posibilități, se alege aceea pentru care numărul de grămezi este mai mare. Dacă există mai multe astfel de soluții, se consideră corectă oricare dintre ele.
c) Monedele care nu au putut fi distribuite conform regulilor stabilite, au fost donate bisericii.

Scrieți un program care determină numărul maxim S de sipete și numărul sipetelor cu p1, p2 respectiv p3 monede, precum și suma donată bisericii.

O firmă de construcţii imobiliare a achiziţionat recent un teren dreptunghiular de dimensiuni N×M. Terenul este împărțit în parcele de dimensiune 1x1. Pe unele dintre cele N×M parcele sunt plantați copaci. Firma dorește construirea unui grandios complex comercial și este necesară defrișarea întregului teren. În acest scop sunt utilizați roboți, fiecare robot având baza un pătrat de latură L. Suprafața defrișată de fiecare robot la un moment dat este chiar aria de acoperire a robotului, L×L. Fiecare robot pătrunde prin colțul stânga sus de coordonate (1, 1), se poate deplasa doar în dreapta și în jos și poate părăsi suprafața numai prin colțul dreapta jos, de coordonate (N, M).

Cunoscând dimensiunile N, M ale terenului și coordonatele parcelelor în care sunt plantați copaci se cere:

1. Numărul minim de roboți necesari defrișării întregului teren.
2. Să se răspundă la Q interogări de forma k, unde k este un număr natural. Pentru fiecare interogare de această formă va trebui determinată latura minimă a unui robot astfel încât să fie necesari pentru defrișare cel mult k roboți.