În această poveste este vorba despre o casă cu mai multe camere. O cameră are forma unui pătrat de latură 1. Dacă două camere au un perete comun, atunci se poate trece dintr-o cameră în alta. Casa nu are neapărat formă dreptunghiulară.

O asemenea casă poate fi descrisă în povestea noastră în două moduri:

• prin matricea minimală: o matrice cu elemente 0 şi 1 în care există N valori egale cu 1, ce corespund camerelor, iar prima linie, ultima linie, prima coloană şi ultima coloană au cel puţin un element egal cu 1.
• prin construcţie: un şir de N-1 perechi (a[i], b[i]) 1≤i<n în care a[i] din {1,2,…,i} şi b[i] din {N, S, E, V}. Camerele vor fi numerotate de la 1 la n. Perechea (a[i], b[i]) precizează poziţia camerei i+1 faţă de camera a[i]: E înseamnă la dreapta (est), N deasupra (nord), V la stânga (vest), S dedesubt (sud). Observaţi că pentru prima cameră nu există nicio precizare!

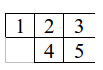
De exemplu, casa de mai sus poate fi descrisă de şirul (1 E) (2 E) (2 S) (3 S), adică a doua cameră e “lipită” la est de prima cameră, următoarea (a treia) la est de camera 2, a patra la sud de camera 2, iar ultima la sud de camera 3.

Cerința

1. Se dă descrierea unei case prin construcţie şi se cere descrierea acesteia prin matricea minimală.
2. Se dă descrierea unei case prin matricea minimală şi se cere descrierea acesteia prin construcţie.

Date de intrare

Fişierul casa.in conţine:

• Pe prima linie un număr natural p reprezentând cerinţa care trebuie rezolvată. Pentru toate testele de intrare, numărul p poate avea valoarea 1 sau 2.
• Dacă valoarea lui p este 1 atunci liniile următoare conţin descrierea unei case prin construcţie astfel: pe linia a doua un număr natural N reprezentând numărul de camere ale casei, iar pe fiecare din următoarele N-1 linii câte două valori separate prin câte un spaţiu – un număr natural şi un caracter, cu semnificaţia de mai sus.
• Dacă valoarea lui p este 2 atunci liniile următoare conţin descrierea unei case prin matrice minimală astfel: pe linia a doua două numere naturale nenule M, N reprezentând dimensiunile matricei, iar pe următoarele M linii câte N numere 0 sau 1 separate prin câte un spaţiu.

Date de ieșire

Dacă valoarea lui p este 1 atunci se va rezolva numai cerinţa 1. În acest caz fişierul casa.out va conţine pe prima linie două numere naturale M şi N, separate prin câte un singur spaţiu reprezentând numărul de linii respectiv numărul de coloane ale matricei minimale, iar pe următoarele M linii câte N valori 0 sau 1 separate prin câte un singur spaţiu.

Dacă valoarea lui p este 2 atunci se va rezolva numai cerinţa 2. În acest caz fişierul casa.out va conţine pe prima linie două numere naturale Nr şi C separate printr-un singur spaţiu. Nr reprezintă numărul de camere, iar C poziţia camerei 1 (cel mai mic număr de ordine al unei coloane care conţine valoarea 1 în prima linie). Următoarele Nr-1 linii vor conţine fiecare câte două valori separate printr-un singur spaţiu, reprezentând descrierea unei case prin construcţie conform precizărilor din enunţ. Coloanele vor fi numerotate începând de la 1, iar dacă există mai multe soluţii va fi afişată cea mai mică în ordine lexicografică: perechea (k, l) va fi afişată înaintea perechii (k’, l’) dacă k < k’ sau dacă k = k’ şi l < l’ (adică E < N < S < V).

Restricții și precizări

• Matricea minimală a unei case are maximum 100000 elemente.

Exemplu:

casa.in

1
5
1 E
2 E
2 S
3 S

casa.out

2 3
1 1 1
0 1 1

Exemplu:

casa.in

2
2 3
1 1 1
1 0 1

casa.out

5 1
1 E
1 S
2 E
4 S