Paftenie trăiește într-un oraș pătratic, împărțit în n x n regiuni pătratice, așezate pe n linii, numerotate de la 1 la n, și n coloane, numerotate de la 1 la n. În fiecare astfel de regiune există o cafenea, iar în dreptul fiecărei cafenele se află un indicator către nord (↑), sud (↓), vest (←) sau est (→). Prin cafeneaua (i, j) ne vom referi la cafeneaua de la linia i și coloana j.

În prima zi, în fiecare cafenea își ia micul dejun exact unul dintre cei n^2 cetățeni ai orașului. Începând cu a doua zi, fiecare cetățean își va lua micul dejun în cafeneaua vecină celei în care și-a luat micul dejun în ziua precedentă, conform direcției de pe indicatorul asociat acesteia. Procesul se repetă timp de k zile.

Pornind într-o zi de la cafeneaua (i, j), cafeneaua vecină la care se ajunge în ziua următoare este (i - 1, j) dacă direcția indicatorului este nord sau (i + 1, j) dacă direcția indicatorului este sud sau (i, j - 1) dacă direcția indicatorului este vest sau (i, j + 1) dacă direcția indicatorului este est.

Paftenie definește gradul de fericire al unui cetățean ca fiind numărul de cetățeni cu care a luat micul dejun împreună cel puțin o dată în timpul celor k zile. Mai mult, Paftenie definește gradul de fericire al orașului drept suma gradelor de fericire ale cetățenilor săi.

Cerința

Cum Paftenie este prea distras de micul său dejun englezesc cu cârnăciori și fasole fiartă, apelează la voi pentru a determina:

1) Numărul maxim de cetățeni care iau micul dejun împreună în cea de-a doua zi.
2) Gradul de fericire al orașului său.

Date de intrare

Fișierul de intrare sim.in conține conține pe prima linie un număr natural C, iar pe a doua linie numerele naturale n și k, separate printr-un spațiu. Următoarele n linii din fișier conțin câte n numere naturale din mulțimea {1, 2, 3, 4} (1 pentru nord, 2 pentru sud, 3 pentru vest, 4 pentru est), separate prin câte un spațiu. Al j-lea număr de pe linia i + 2 din fișier reprezintă direcția indicatorului asociat cafenelei (i, j).

Date de ieșire

Fișierul de ieșire sim.out va conține un singur număr natural X:

• Dacă C = 1, atunci X va fi numărul maxim de cetățeni care iau micul dejun împreună în cea de-a doua zi.
• Dacă C = 2, atunci X va fi gradul de fericire al orașului lui Paftenie.

Restricții și precizări

• C ∊ {1, 2}
• 2 ≤ n ≤ 1.000
• k ∊ {1.000, 1.000.000.000}
• Se garantează că nu există niciun indicator care, odată urmat, duce la părăsirea orașului.
• Pentru 20 de puncte, C = 1, n ≤ 30, k = 1.000
• Pentru 30 de puncte, C = 2, n ≤ 30, k = 1.000
• Pentru 20 de puncte, C = 2, n ≤ 30, k = 1.000.000.000
• Pentru 30 de puncte, C = 2, 30 < n ≤ 1.000, k = 1.000.000.000

Exemplul 1:

sim.in

1
3 1000
4 3 2
4 2 2
4 3 3

sim.out

3

Explicație

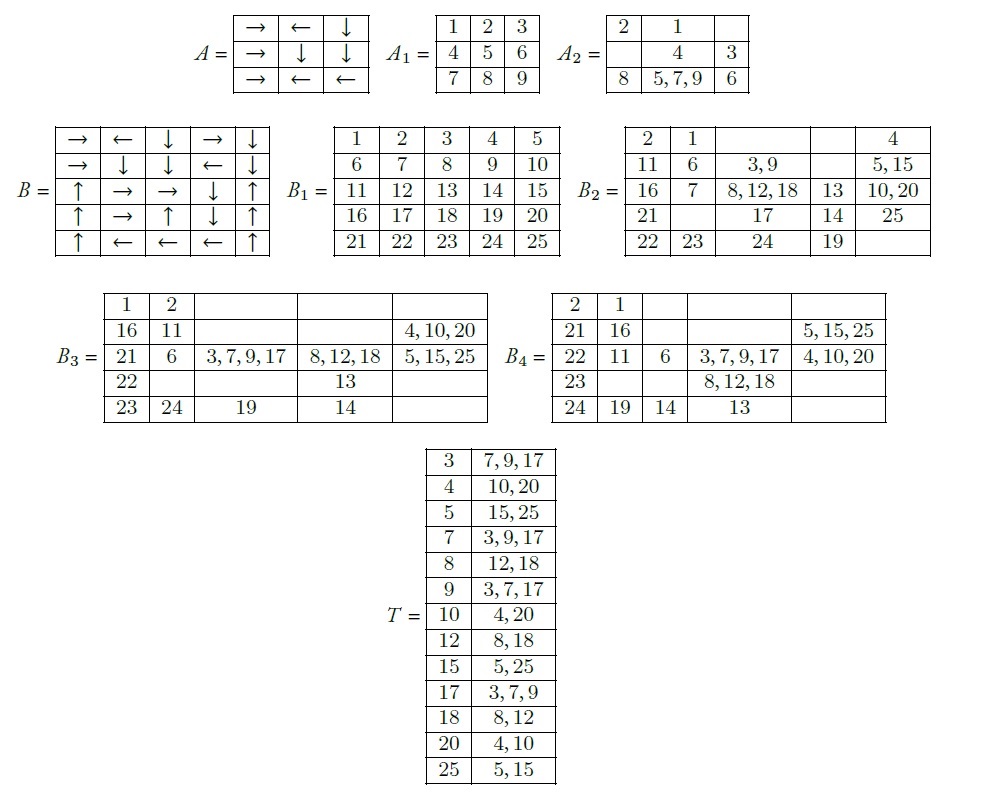
Orașul este reprezentat grafic în tabloul bidimensional (matricea) A, iar cetățenii săi sunt numerotați precum în matricea A1. În fiecare celulă a matricei Ai, cu 1 ≤ i ≤ 2, sunt cetățenii care, în ziua i, iau micul dejun în cafeneaua respectivă. Numărul maxim de cetățeni care iau masa împreună în a doua zi este 3, aceștia fiind situați în cafeneaua (3, 2).

Exemplul 2:

sim.in

25
1000
4 3 2 4 2
4 2 2 3 2
1 4 4 2 1
1 4 1 2 1
1 3 3 3 1

sim.out

30

Explicație

Orașul este reprezentat grafic în tabloul bidimensional (matricea) B, iar cetățenii săi sunt numerotați precum în matricea B1. În fiecare celulă a matricei Bi, cu 1 ≤ i ≤ 4, sunt cetățenii care, în ziua i, iau micul dejun în cafeneaua respectivă. Tabelul T conține întâlnirile care au loc până la finalul celor 1000 de zile. A doua coloană conține lista cetățenilor cu care se întâlnește cetățeanul din prima coloană. Răspunsul este 3 + 2 + 2 + 3 + 2 + 3 + 2 + 2 + 2 + 3 + 2 + 2 + 2 = 30.