Se consideră n copaci de diferite înălţimi, aflaţi în linie dreaptă la distanţe egale, numerotaţi de la 1 la n. Pentru fiecare copac se cunoaşte înălţimea sa \( {H}_{i} \). Cum şi copacii simt nevoia să socializeze, fiecare dintre ei are prieteni printre ceilalţi copaci. Prietenii oricărui copac i se pot afla atât la stânga, cât şi la dreapta sa. Relaţiile de prietenie sunt definite în felul următor: pentru fiecare copac i considerăm un şir \( {d}_{1}, {d}_{2}, …, {d}_{x} \) reprezentând prietenii copacului i situaţi în dreapta sa şi un şir \( {s}_{1}, {s}_{2}, …, {s}_{y} \) reprezentând prietenii copacului i situaţi în stânga acestuia. Copacii din cele două şiruri corespunzătoare unui copac i formează împreună lista prietenilor acestuia. Şirurile corespunzătoare copacului i se definesc astfel:

1. \( {d}_{1} = i + 1 \) (dacă i = n, atunci copacul i nu are niciun prieten la dreapta sa, şirul rămânând vid). Pentru fiecare k ≥ 2, \( {d}_{k} \) este cel mai mic indice (\( 1 ≤ {d}_{k} ≤ n \)) cu proprietatea că \( {d}_{k} > {d}_{k-1} \) şi \( {H}_{{d}_{k}} > {H}_{{d}_{k-1}} \). Dacă \( {d}_{k} \) nu există, atunci lista de prieteni la dreapta ai copacului i s-a încheiat şi construirea şirului se opreşte la acest pas.
2. \( {s}_{1} = i – 1 \) (dacă i = 1, atunci copacul i nu are niciun prieten la stânga sa, şirul rămânând vid). Pentru fiecare k ≥ 2, \( {s}_{k} \) este cel mai mare indice (\( 1 ≤ {s}_{k} ≤ n \)) cu proprietatea că \( {s}_{k} < {s}_{k-1} \) şi \( {H}_{{s}_{k}} > {H}_{{s}_{k-1}} \). Dacă \( {s}_{k} \) nu există, atunci lista de prieteni la stânga ai copacului i s-a încheiat şi construirea şirului se opreşte la acest pas.

De exemplu, în figura de mai jos sunt reprezentaţi 7 copaci, fiecare având precizată sub el valoarea

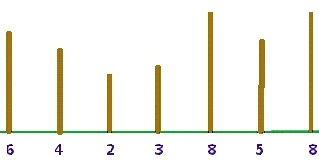
Copacul 1 este prieten cu copacul 2 fiind vecini, cu copacul 5 (deoarece copacul 5 este primul din dreapta lui 2 cu înălţimea mai mare strict decât înălţimea lui 2). La dreapta copacului 5 nu există niciun copac cu înălţimea mai mare strict decât a sa, deci singurii prieteni ai copacului 1 sunt 2 şi 5.

Pentru copacul 3, prietenii la stânga sa sunt copacii 2 şi 1, iar cei de la dreapta sa sunt copacii 4 şi 5. Pentru copacul 6, singurul prieten la stânga este copacul 5, iar la dreapta copacul 7.

Copacul 7 poate avea prieteni doar la stânga, aceştia sunt 6 şi 5 (la stânga copacului 5 nu mai există niciun copac cu înălţimea mai mare strict decât 8).

Grădinarul Marian vrea să aleagă 3 copaci diferiţi dintre cei n pentru a-i planta în altă grădină. El doreşte ca dintre cei 3 copaci, oricum ar alege A si B, 2 dintre ei, atunci A este prieten cu B şi B este prieten cu A (relaţiile de prietenie se consideră cele stabilite iniţial). Marian are mai multe opţiuni şi se întreabă în câte moduri distincte poate alege cei 3 copaci cu proprietatea cerută.

Cerința

Determinaţi în câte moduri se pot alege 3 copaci diferiţi dintre cei n cu proprietatea că, oricum am alege 2 copaci dintre cei 3, fie aceştia copacul A şi copacul B, atunci A este prieten cu B şi B este prieten cu A.

Date de intrare

Fişierul de intrare copaci1.in conţine pe prima linie un număr natural n, reprezentând numărul de copaci, iar pe a doua linie n numere naturale nenule, separate prin câte un spaţiu, reprezentând înălţimile copacilor.

Date de ieșire

Fişierul de ieşire copaci1.out va conţine pe prima linie un număr natural reprezentând numărul de moduri în care Marian poate alege 3 copaci cu proprietatea din enunţ.

Restricții și precizări

• 1 ≤ n ≤ 200 000;
• \( 1 ≤ {H}_{i} ≤ 200\);
• nu vor exista 2 copaci alăturaţi cu aceeaşi înălţime;
• două triplete de copaci se consideră distincte dacă există cel puţin un copac din primul triplet care nu se află şi în al doilea triplet;
• pentru 30% din teste, 1 ≤ n ≤ 200.

Exemplu:

copaci1.in

7
6 4 2 3 8 5 8

copaci1.out

4

Explicație

Copacul 1 este prieten cu copacii: 2 5
Copacul 2 este prieten cu copacii: 1 3 4 5
Copacul 3 este prieten cu copacii: 1 2 4 5
Copacul 4 este prieten cu copacii: 1 2 3 5
Copacul 5 este prieten cu copacii: 1 2 4 6 7
Copacul 6 este prieten cu copacii: 5 7
Copacul 7 este prieten cu copacii: 5 6
Modurile în care Marian poate alege cei 3 copaci sunt:
(1, 2, 5), (2, 4, 5), (2, 3, 4), (5, 6, 7).