Tablouri patratice

Un tablou bidimensional este tablou pătratic sau matrice pătratică dacă numărul de linii este egal cu numărul de coloane.

În această situație folosim pentru ambele dimensiuni o singură variabilă, de regulă n:

int n, A[100][100];

Exemplu:

Matrice pătratică indexată de la 0	Matrice pătratică indexată de la 1

Într-o matrice pătratică se disting o categorie specială de elemente, diagonalele. Un element al matricei aparține sau nu diagonalelor sau zonelor delimitate de acestea dacă respectă anumite reguli, în care intervin indicii elementului, nu valoarea elementului. În cele ce urmează, pentru un element oarecare al matricei vom nota cu i indicele de linie și cu j indicele de coloană.

Diagonala principală

Indexare de la 0	Indexare de la 1
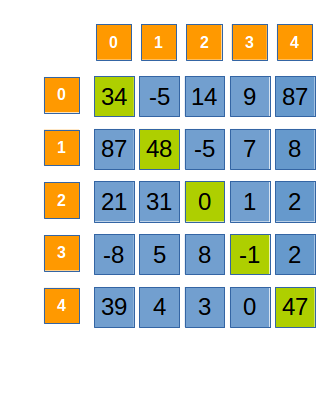i = j	i = j

Parcurgerea elementelor de pe diagonala principală:

for(int i = 0 ; i < n ; i ++)
{
    // A[i][i]
}

Diagonala secundară

Indexare de la 0	Indexare de la 1
i + j = n - 1	i + j = n + 1

Parcurgerea elementelor de pe diagonala secundară:

//indexare de la 0
for(int i = 0 ; i < n ; i ++)
{
    // A[i][n - 1 - i]
}

//indexare de la 1
for(int i = 1 ; i <= n ; i ++)
{
    // A[i][n + 1 - i]
}

Observație: Dacă n este impar, cele două diagonale au un element comun. Dacă n este par, cele două diagonale nu au elemente comune.

---

Elementele delimitate de diagonala principală

Deasupra diagonalei		Sub diagonală
Indexare de la 0	Indexare de la 1	Indexare de la 0	Indexare de la 1
i < j		i > j

Elementele delimitate de diagonala secundară

Deasupra diagonalei		Sub diagonală
Indexare de la 0	Indexare de la 1	Indexare de la 0	Indexare de la 1
i + j < n - 1	i + j < n + 1	i + j > n - 1	i + j > n + 1

Zonele delimitate de diagonale

Cele două diagonale delimitează în matrice patru zone: Nord, Est, Sud și Vest. Condițiile verificate de indicii elementelor din aceste zone sunt prezentate mai jos: