Cerința

Se dă un arbore cu \(N\) noduri și \(N-1\) muchii etichetate cu o literă fiecare. Vom defini un drum \((x, y)\) ca fiind secvența de muchii care duc de la nodul \(x\) la nodul \(y\). De asemenea, vom considera drumurile \((x, y)\) si \((y, x)\) ca fiind același drum. Un drum poate fi palindromic dacă există o cale de a permuta toate literele parcurse in drumul respectiv în așa fel încât să formăm un drum palindromic.

Să se afle câte drumuri pot fi palindromice.

Date de intrare

Pe prima linie se va afla numărul \(N\), reprezentând numărul de noduri.

Pe următoarele \(N-1\) linii se va afla câte un triplet \(a \ b \ ch\), reprezentând muchia de la nodul \(a\) la nodul \(b\), etichetată cu caracterul \(ch\).

Date de ieșire

Se va afișa pe o linie numărul de drumuri care pot fi palindromice.

Restricții și precizări

• \(1 \leq N \leq 100 \ 000\)

Exemplu:

Intrare

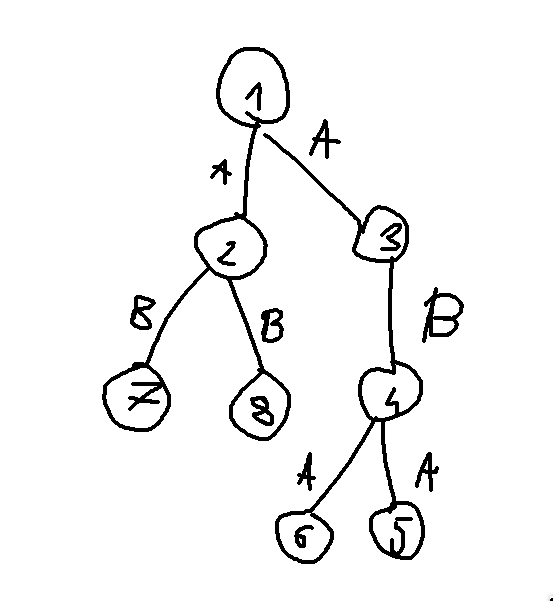
8
1 2 a
1 3 a
2 7 b
2 8 b
3 4 b
4 5 a
4 6 a

Ieșire

21

Explicație

Drumurile care pot fi palindromice sunt: \((1, 2)\), \((1, 3)\), \((1, 5)\), \((1, 6)\), \((2, 3)\), \((2, 4)\), \((2, 7)\), \((2, 8)\), \((3, 4)\), \((3, 7)\), \((3, 8)\), \((4, 5)\), \((4, 6)\), \((4, 7)\), \((4, 8)\), \((5, 6)\), \((5, 7)\), \((5, 8)\), \((6, 7)\), \((6, 8)\), \((7, 8)\).