Fie un graf neorientat conex, având cele N noduri numerotate de la 1 la N. Se realizează parcurgerea în adâncime a grafului pornind din nodul 1. Dacă există mai mulţi adiacenţi ai săi nevizitaţi, atunci se alege ca nod succesor cel de indice cel mai mic. În continuare se respectă aceeaşi regulă, adică dacă nodul curent este x, se alege dintre toate nodurile adiacente cu x şi nevizitate acela de indice minim. Dacă x nu are adiacenţi, se merge înapoi la nodul precedent lui x pentru a se căuta un adiacent nevizitat.

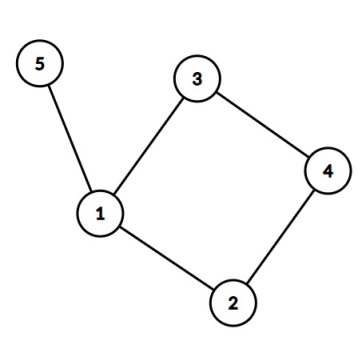
De exemplu, pentru graful din figură, parcurgând graful în adâncime începând cu nodul 1 şi respectând regulile de mai sus, ordinea vizitării nodurilor este: 1 2 4 3 5.

Cerința

Scrieţi un program care să determine numărul maxim de muchii care pot fi adăugate grafului astfel încât ordinea de vizitare a nodurilor prin parcurgerea în adâncime să rămână aceeaşi.

Date de intrare

Fișierul de intrare dfs.in conține pe prima linie un număr natural N reprezentând numărul de noduri din graf. Pe linia a doua se află un singur număr natural M reprezentând numărul muchiilor grafului. Pe următoarele M linii se găsesc câte două numere naturale x şi y, separate printr-un spaţiu, reprezentând câte o muchie din graf.

Date de ieșire

Fișierul de ieșire dfs.out va conține un singur număr natural reprezentând numărul maxim de muchii care se pot adăuga grafului astfel încât ordinea parcurgerii în adâncime a nodurilor să fie aceeaşi.

Restricții și precizări

• 1 ≤ n ≤ 1000

Exemplu:

dfs.in

5
5
1 5
1 3
2 1
3 4
4 2

dfs.out

4

Explicație

Fişierul de intrare corespunde grafului din imagine. Se pot adăuga maximum 4 muchii: (1,4), (2,5), (3,5), (4,5) şi după adăugare, parcurgerea în adâncime pornind din nodul 1 este tot 1 2 4 3 5.