Moldovan Robert (use KN) (moldovan_robert_lol) Cerința
Se dă o expresie aritmetică care folosește paranteze și operatorii \(+\) (adunare), \(-\) (scădere), \(*\) (înmulțire) și \(/\) (împărțire) în funcție de cerință:
- \(1\) – se dă o expresie prefixată
- \(2\) – se dă o expresie postfixată
- \(3\) – se dă o expresie infixată
Să se afișeze toate celelalte forme ale expresiei. De exemplu, dacă cerința este \(1\), se vor afișa expresiile postfixate și infixate ș.a.m.d.
Date de intrare
Pe prima linie se va afla numărul natural \(\text{cer}\), iar pe a doua linie se va afla expresia.
Date de ieșire
Dacă cerința este \(1\):
- se va afișa pe prima linie expresia postfixată
- se va afișa pe a doua linie expresia infixată
Dacă cerința este \(2\):
- se va afișa pe prima linie expresia prefixată
- se va afișa pe a doua linie expresia infixată
Dacă cerința este \(3\):
- se va afișa pe prima linie expresia prefixată
- se va afișa pe a doua linie expresia postfixată
Restricții și precizări
- în expresie nu vor exista spații
- expresia este alcătuită din paranteze, operatorii mentionați mai sus și din litere mici din alfabetul englez
- se garantează că expresia dată este corectă
- pentru formele infixate afișate, se va afișa varianta fără paranteze inutile
- lungimea expresiei din fișierul de intrare va fi mai mică sau egală cu \(200 \ 000\)
Punctare
- Cerința \(1\): \(30 \text{p}\)
- Cerința \(2\): \(30 \text{p}\)
- Cerința \(3\): \(40 \text{p}\)
Exemplu \(1\):
Intrare
1 +ab
Ieșire
ab+ a+b
Exemplu \(2\):
Intrare
2 ab+
Ieșire
+ab a+b
Exemplu \(3\):
Intrare
3 a+b
Ieșire
+ab ab+
Exemplu \(4\):
Intrare
3 a+b*c
Ieșire
+a*bc abc*+
Exemplu \(5\):
Intrare
3 (a+b)*c
Ieșire
3 *+abc ab+c*
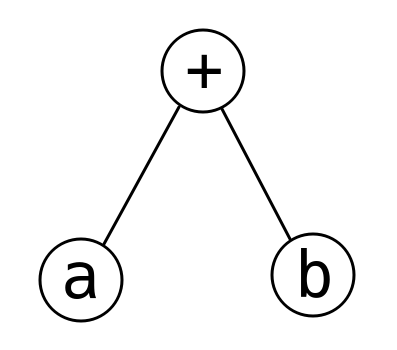
Explicație \(1 \ – \ 3\)
Arborele corespunzător expresiei din exemplele \(1 \ – \ 3\):
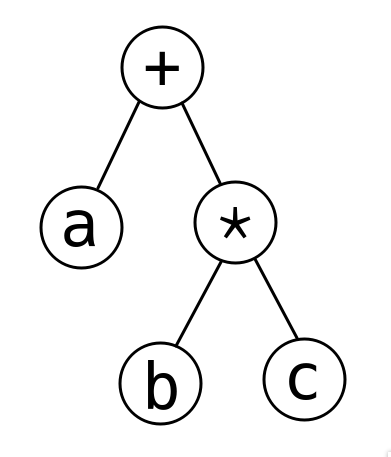
Explicație \(4\)
Arborele corespunzător expresiei din exemplul \(4\):
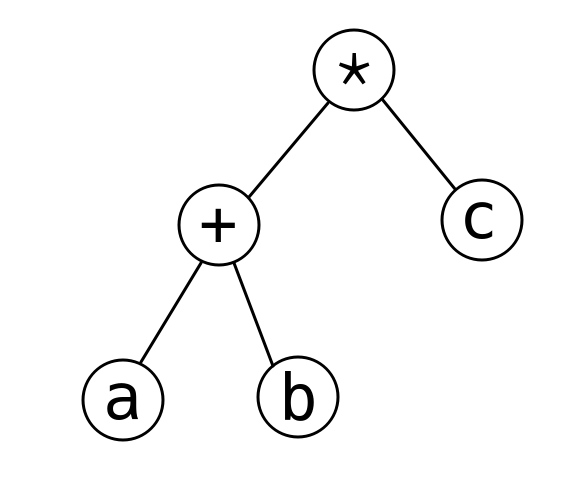
Explicație \(5\)
Arborele corespunzător expresiei din exemplul \(5\):
