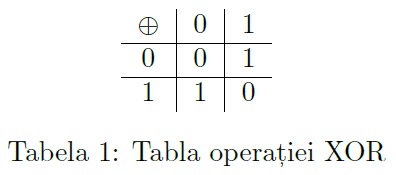
Se dă o permutare A a numerelor de la 1 la N. Operatorul ⊕ din limbajul C/C++ realizează operația XOR (disjuncție exclusivă pe biți).
Cerința
Scrieți un program care să rezolve următoarele două cerințe:
1. Construiți o altă permutare B astfel încât expresia E = (A1 + B1) ⊕ (A2 + B2) ⊕ ... ⊕ (AN + BN) să aibă valoare minimă.
2. Construiți o altă permutare B astfel încât expresia E = (A1 + B1) ⊕ (A2 + B2) ⊕ ... ⊕ (AN + BN) să aibă valoare maximă.
Date de intrare
Fișierul de intrare sumxor.in conține pe prima linie numărul C care poate avea valoarea 1 sau 2 în funcție de cerința ce trebuie rezolvată. Pe a doua linie se va afla numărul N, iar pe a treia linie se vor afla N numere distincte cuprinse între 1 și N, reprezentând permutarea A.
Date de ieșire
Fișierul de ieșire sumxor.out va conține pe prima linie valoarea expresiei E în funcție de cerință (pentru cerința 1 se va afișa minimul, iar pentru cerința 2 se va afișa maximul). Pe a doua linie se vor afișa N numere distincte cuprinse între 1 și N, separate prin câte un spațiu reprezentând o permutare B cu ajutorul căreia se obține valoarea E.
Restricții și precizări
1 ≤ N ≤ 1.000.0001 ≤ Ai ≤ N,Ai ̸≠ Ajpentru oricei ̸≠ j- Dacă există mai multe șiruri
Bcare satisfac condițiile, puteți afișa oricare dintre ele. - Pentru 16 puncte,
C = 1,1 ≤ N ≤ 10 - Pentru 16 puncte,
C = 2, 1 ≤ N ≤ 10 - Pentru 23 de puncte,
C = 1 - Pentru 45 de puncte,
C = 2 - Datorită dimensiunilor mari, nu au putut fi adăugate toate testele.
Exemplul 1:
sumxor.in
1 2 2 1
sumxor.out
0 1 2
Explicație
E = (2 + 1) ⊕ (1 + 2) = 3 ⊕ 3 = 0. Aceasta este valoarea minimă ce se poate obține.
Exemplul 2:
sumxor.in
2 5 4 3 1 5 2
sumxor.out
14 5 4 3 2 1
Explicație
E = (4 + 5)⊕(3 + 4)⊕(1 + 3)⊕(5 + 2)⊕(2 + 1) = 9 ⊕ 7 ⊕ 4 ⊕ 7 ⊕ 3 = 14. Se poate demonstra că nu se poate obține o valoare mai mare în acest caz.