Mark a construit o parcare dreptunghiulară, pe care a împărțit-o, utilizând marcaje, în locuri de parcare pătrate, organizate pe n linii (numerotate de la 1 la n) și m coloane (numerotate de la 1 la m). Astfel, un loc de parcare poate fi identificat prin numărul liniei şi numărul coloanei pe care acesta se află. Orice mașină poate fi parcată în interiorul unui loc de parcare, paralel cu liniile orizontale de marcaj, sau paralel cu liniile verticale, fără a depăși conturul pătratului corespunzător. Mark a construit un zid de împrejmuire a parcării, întrerupt în dreptul unor locuri de parcare, pentru a permite ieșirea mașinilor din parcare. Considerăm că zidul este plasat pe linia 0 (nord), coloana 0 (vest), linia n+1 (sud) şi coloana m+1 (est).

O mașină parcată paralel cu marcajele orizontale se poate deplasa pe linie, spre stânga sau spre dreapta, putând ieși din parcare dacă ajunge la o întrerupere a zidului de la vest sau de la est, și doar dacă nu există o nicio altă maşină parcată în sensul ei de deplasare către ieşire. O mașină parcată paralel cu marcajele verticale se poate deplasa pe coloană în sus sau în jos, putând ieși din parcare dacă ajunge la o întrerupere a zidului de la spre nord sau de la sud, și doar dacă nu există nicio altă maşină parcată în sensul ei de deplasare către ieşire. Mașinile se pot deplasa mergând în față sau în marșarier. De exemplu, mașina parcată în locul (2,2) paralel cu marcajele orizontale, nu poate ieși din parcare, deoarece dacă se deplasează spre vest ajunge la zid, iar dacă se deplasează spre est, nu poate ajunge la întreruperea din zid corespunzătoare acelei linii din cauza altor mașini parcate pe traseu, dar maşina din locul (2,6) poate ieşi deplasându-se spre est.

Ieșirea din parcare se face în serii consecutive, maşinile dintr-o serie începând deplasarea simultan (după ce au ieșit toate mașinile din seria anterioară); din seria curentă fac parte toate mașinile care, exact la acel moment, au drumul liber spre cel puțin o întrerupere de zid (nu este necesară mișcarea niciunei alte mașini rămase în parcare, inclusiv a celor din seria curentă), chiar dacă traseul lor către ieșire se intersectează cu traseul altor mașini din aceeași serie, aflate în deplasare. În prima serie ies toate mașinile care pot pleca din parcare imediat, fără a fi condiționate de mutarea sau părăsirea parcării de către alte mașini.

Cerința

Scrieți un program care, cunoscând dimensiunile parcării, pozițiile întreruperilor din zid, numărul de mașini, iar pentru fiecare mașină numărul liniei și al coloanei corespunzătoare locului în care este parcată și modul de parcare a acesteia, rezolvă următoarele două cerinţe:
1) determină numărul de mașini care pot ieși din parcare fără a fi condiționate de mutarea sau de părăsirea parcării de către alte mașini (numărul de maşini care pot ieşi în prima serie);
2) determină numărul total maşini care pot ieşi din parcare, precum şi numărul de serii în care se realizează ieşirea tuturor acestor maşini.

Date de intrare

Fișierul de intrare parking.in conține pe prima linie numerele naturale c, n, m, k și q reprezentând, în ordine, numărul cerinței, numărul de linii și numărul de coloane ale parcării, numărul de întreruperi ale zidului parcării, respectiv, numărul de mașini parcate. Pe următoarele k linii se află câte două numere naturale i și j reprezentând pozițiile (linia, respectiv coloana) întreruperilor din zidul parcării. Pe următoarele q linii se află câte trei numere naturale x, y și p reprezentând, în ordine, numărul liniei și al coloanei corespunzătoare locului în care este parcată o mașină și modul de parcare a acesteia (p=0 pentru parcare paralelă cu marcajele orizontale, respectiv p=1 pentru parcare paralelă cu marcajele verticale). Valorile scrise pe aceeaşi linie sunt separate prin câte un spaţiu.

Date de ieșire

Fișierul de ieșire parking.out va conține o singură linie ce va conține:

• numărul de maşini care au ieşit din parcare în prima serie, dacă c=1;
• numărul total de mașini care au ieşit din parcare și numărul de serii în care s-a realizat ieşirea maşinilor, separate printr-un spaţiu, dacă c=2.

Restricții și precizări

• 2 ≤ n, m ≤ 1000
• 2 ≤ k ≤ 2 • n + 2 • m
• 2 ≤ q ≤ min(n • m, 100.000)
• 1 ≤ i ≤ n, pentru j=0 sau j=m+1 şi 1 ≤ j ≤ m, pentru i=0 sau i=n+1
• 1 ≤ x ≤ n, 1 ≤ y ≤ m, 0 ≤ p ≤ 1
• Se garantează pentru datele de test că numărul de serii obținute va fi cel mult 10.000, dacă c=2.
• Pe parcursul deplasării pentru a ieși din parcare mașinile vor circula astfel încât nu se vor ciocni.
• Pentru 12 puncte, C=1, n, m, q ≤ 150
• Pentru 16 puncte, C=1 și nu există restricții suplimentare.
• Pentru 12 puncte, C=2, n, m, q ≤ 150
• Pentru 60 puncte, C=2 și nu există restricții suplimentare.

Exemplul 1:

parking.in

1 6 7 11 16
0 1
0 4
0 6
7 2
7 3
7 5
7 7 
1 0
4 0
6 0
2 8
1 2 1
1 4 0
2 2 0
2 4 1
2 6 0
3 1 1
3 4 0
3 6 1
4 2 0
4 3 1
4 5 0
4 7 1
5 6 0
6 1 0
6 3 1
6 6 0

parking.out

6

Explicație

Datele corespund imaginii din enunț. Pot ieși din parcare fără a aștepta mutarea sau plecarea altor mașini cele 6 mașini aflate în locurile de parcare din pozițiile:
(2,6) – spre est
(3,1) – spre nord
(4,2) – spre vest
(4,7) – spre sud
(6,1) – spre vest
(6,3) – spre sud

Exemplul 2:

parking.in

2 6 7 11 16
0 1
0 4
0 6
7 2
7 3
7 5
7 7 
1 0
4 0
6 0
2 8
1 2 1
1 4 0
2 2 0
2 4 1
2 6 0
3 1 1
3 4 0
3 6 1
4 2 0
4 3 1
4 5 0
4 7 1
5 6 0
6 1 0
6 3 1
6 6 0

parking.out

10 3

Explicație

Seria 1: ies din parcare cele 6 mașini, specificate la exemplul precedent.
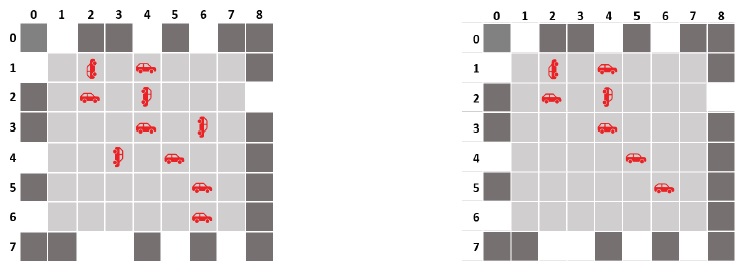
Seria 2: pot ieși din parcare cele 3 mașini aflate în locurile de parcare din pozițiile: (3, 6) – spre nord, (4, 3) – spre sud, (6, 6) – spre vest. Configurația apare în prima imagine de mai jos.
Seria 3: poate ieși din parcare o singură mașină aflată în locul de parcare din poziția: (4,5) – spre vest. Vor putea părăsi parcarea în total 6 + 3 + 1 = 10 mașini în 3 serii. Configurația apare în a doua imagine de mai jos.