Cerința
Prietenii lui RAU-Gigel vor să-i facă o surpriză de ziua lui! Pentru aceasta, ei trebuie să se întâlnească într-un singur loc pentru a se putea organiza mai eficient.
RAU-Gigel are N prieteni, etichetați în continuare cu numere de la 1 la N, ale căror poziții le putem reprezenta drept puncte în plan de coordonate numere naturale nenule, care sunt, pentru simplitate, tot de la 1 la N. Aceștia doresc să se întâlnească într-un singur punct de coordonate numere naturale nenule. În acest scop, fiecare prieten poate face câte un pas de lungime unitară (raportat la un reper cartezian în care s-ar putea reprezenta punctele) în oricare din cele 4 direcții cardinale (Nord, Est, Sud sau Vest) de oricâte ori dorește. Se consideră că distanța parcursă de un prieten până la locul de întâlnire este egală cu numărul de pași parcurși de acesta pentru a ajunge la respectiva destinație.
În urma unei discuții aprinse s-a ajuns la un compromis care să mulțumească pe toată lumea și s-a hotărât ca prietenii personajului nostru principal să se întâlnească într-unul din punctele (nu neapărat din cele N date) care minimizează suma distanțelor minime de la fiecare prieten la punctul respectiv ales (prietenilor lui RAU-Gigel nu le place sportul, deci vor parcurge mereu drumul de lungime minimă până la punctul de întâlnire stabilit).
Pentru că prietenii lui RAU-Gigel au o perioadă mai încărcată (BAC, admitere, …) nu își pot potrivi programul perfect pentru a se întâlni mereu cu toții, așa că organizează mai multe întâlniri la care vor participa prieteni dintr-un interval continuu de indici pe baza numerotării stabilite inițial. Pentru fiecare astfel de întâlnire se vrea să se afle (din motive pur statistice) care este suma minimă a tuturor distanțelor parcurse de către prieteni până la punctul de întâlnire, dacă acesta este ales optim.
Această veritabilă problemă de informatică a fost prea grea pentru prietenii lui RAU-Gigel și pentru că nu pot apela la acesta să o rezolve (pentru a nu risca să strice surpriza), îți cer ție, știind că ești un informatician iscusit, să-i ajuți cât mai rapid (deoarece ziua de naștere se apropie), răsplătindu-te astfel dacă vei reuși cu cât mai multe puncte la concursul tău favorit de programare!
Date de intrare
Fișierul de intrare meeting.in conține pe prima linie numărul N, iar pe următoarele N linii câte 2 numere naturale nenule \( {x}_{i}, {y}_{i} \), reprezentând coordonatele punctului aferent prietenului cu numărul i.
Pe următoarea linie se citește un număr Q, iar pe următoarele Q linii câte 2 numere naturale nenule \( {l}_{i}, {r}_{i} \), reprezentând câte un interval de prieteni care vor participa la întâlnirea cu numărul i.
Date de ieșire
Fișierul de ieșire meeting.out va conține pe primele Q linii câte un număr care reprezintă suma minimă a tuturor distanțelor parcurse de către prietenii din intervalul dat până la punctul de întâlnire, dacă acesta este ales optim.
Restricții și precizări
- \( 1 ≤ N, Q < {2}^{17} \)
- \( 1 ≤ {x}_{i}, {y}_{i} ≤ N \)
- \( 1 ≤ {l}_{i} ≤ {r}_{i} ≤ N \)
- Atenție! Punctul în care prietenii se întâlnesc nu trebuie să fie neapărat unul dintre cele
Npuncte în care se află aceștia inițial, dar ar putea fi! De asemenea, coordonatele acestuia trebuie să fie numere naturale nenule (în mod evident, prietenii lui RAU-Gigel nu pot ajunge în puncte care nu au coordonate întregi, plecând din puncte de coordonate numere naturale nenule și efectuând doar pași de lungime1). - Atenție! Dacă doi sau mai mulți prieteni parcurg la un moment dat o bucată de drum comună (execută aceeași pași din aceleași puncte), aceasta contribuie individual la traseul fiecăruia, fiind astfel adunată de mai multe ori la suma cerută, pentru că apare în mai multe trasee.
- Pentru teste în valoare de
5puncte, \( 1 ≤ N, Q < {2}^{7} \) - Pentru alte teste în valoare de
10puncte, \( 1 ≤ N, Q < {2}^{9} \) - Pentru alte teste în valoare de
10puncte, \( 1 ≤ N, Q < {2}^{11} \) - Pentru alte teste în valoare de
15puncte, \( 1 ≤ N < {2}^{17} \) și \(1 ≤ Q < {2}^{8} \) - Pentru alte teste în valoare de
15puncte, \( 1 ≤ N < {2}^{11} \) și \( 1 ≤ Q < {2}^{17} \) - Pentru alte teste în valoare de
15puncte, \( 1 ≤ N, Q < {2}^{15} \) - Pentru alte teste în valoare de
15puncte, \( 1 ≤ N, Q < {2}^{16} \) - Pentru restul testelor nu există restricții suplimentare, adică se păstrează doar condiția \( 1 ≤ N, Q < {2}^{17} \)
Exemplu:
meeting.in
7 2 3 1 4 5 5 4 3 3 6 1 2 7 4 5 1 7 3 5 4 7 2 6 2 5
meeting.out
19 5 12 13 9
Explicație
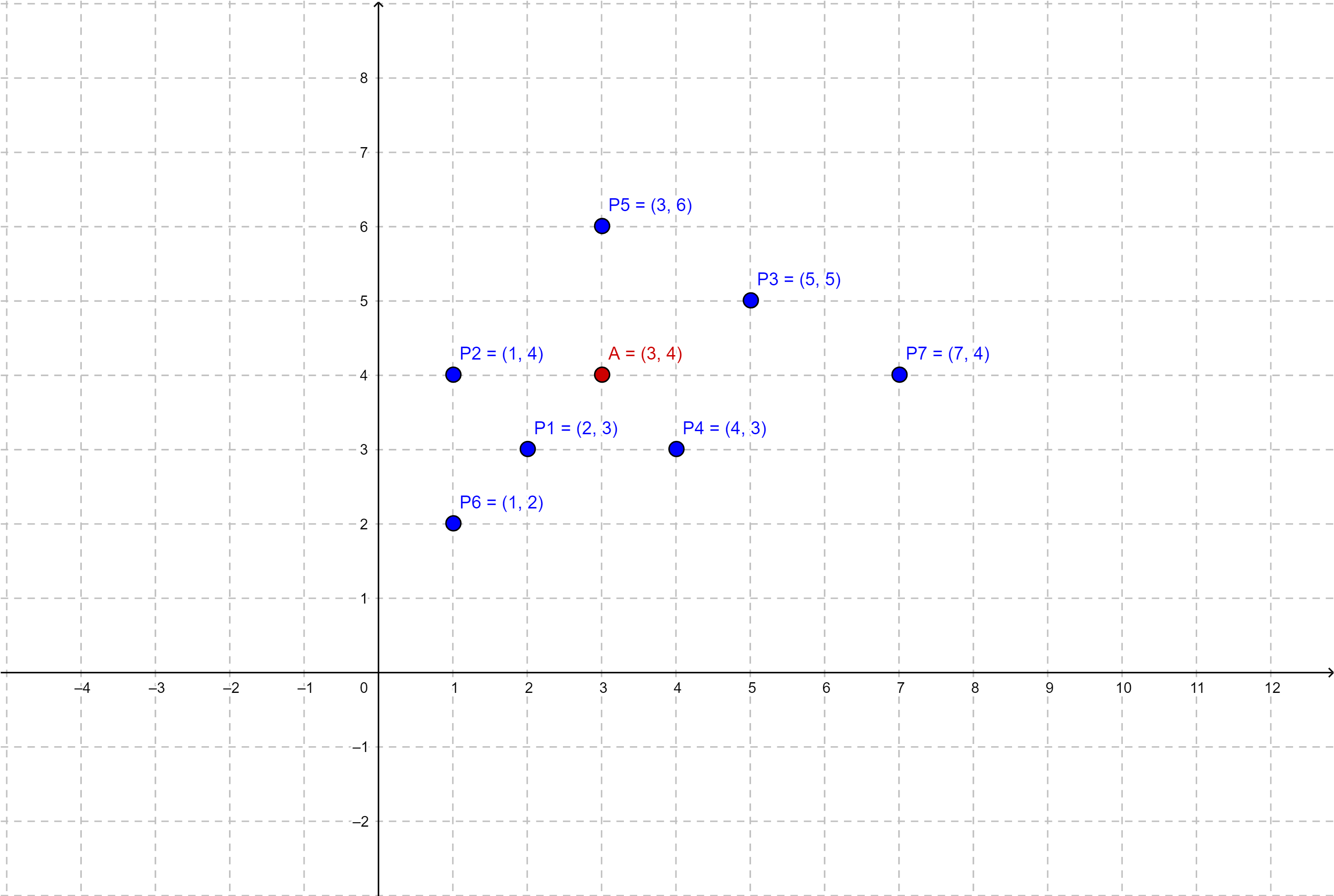
Pentru prima interogare din exemplu se poate demonstra că punctul A(3, 4) este optim, acesta minimizând suma distanțelor minime de la restul punctelor la acesta. Dacă notăm cu D(X, Y) distanța minimă dintre punctele X și Y, atunci D(P1, A) = 2, D(P2, A) = 2, D(P3, A) = 3, D(P4, A) = 2, D(P5, A) = 2, D(P6, A) = 4, D(P7, A) = 4, suma fiind astfel 2 + 2 + 3 + 2 + 2 + 4 + 4 = 19. Pentru restul interogărilor din exemplu se procedează similar.