Vasile este un tânăr programator angajat recent la o firma oarecare din domenul IT. Deoarece câştigă foarte bine el şi-a achiziţionat un teren de formă dreptunghiulară. Colţurile dreptunghiului care definesc acest teren au coordonatele (0,0), (N,M), unde N şi M sunt numere naturale.

Pe acest teren Vasile doreşte să construiască în primul rând o piscină de arie maximă, de formă dreptunghiulară, cu laturile respectiv paralele cu cele ale terenului.

Deşi credea că şi-a îndeplinit visul, Vasile şi-a dat seama că în viaţă nimic nu este atât de uşor deoarece au apărut două restricţii pe care el trebuie să le respecte:

• Deoarece alimentarea cu apă se poate face doar în colţurile dreptunghiului care reprezintă terenul, piscina trebuie să aibă un punct comun cu unul dintre punctele (0,0),(0,M),(N,0) sau (N,M).
• Pe teren se află P pomi la coordonate întregi cunoscute. Aceştia nu pot face parte din dreptunghiul ce defineşte piscina. Iar Vasile nici nu se gândeşte să taie vreun copac pentru că îi place aerul curat. Copacii se pot afla însă pe marginea piscinei.

Cerința

Scrieţi un program care determină aria maximă pe care o poate avea piscina respectând restricţiile din enunţ.

Date de intrare

Fişierul de intrare piscina.in conţine pe prima linie două numere naturale N şi M ce reprezintă dimensiunile laturilor terenului. Pe următoarea linie se află numărul natural P ce preprezintă numărul de copaci care se află pe teren. Următoarele P linii conţin câte două numere Xi şi Yi, separate printr-un spaţiu, reprezentând coordonatele fiecărui copac.

Date de ieșire

Fişierul piscina.out va conţine o singură linie cu un singur număr întreg reprezentând suprafaţa piscinei de arie maximă.

Restricții și precizări

• 1 ≤ N, M ≤ 500000
• 3 ≤ P ≤ 100000
• 0 < Xi < N, 0 < Yi < M iar Xi şi Yi sunt numere întregi
• Valorile Xi sunt distincte
• Valorile Yi sunt distincte
• Pentru teste în valoare de 30 puncte: P ≤ 100
• Pentru teste în valoare de 60 puncte: P ≤ 5000

Exemplu:

piscina.in

5 7
4
1 2
2 1
3 5
4 6

piscina.out

15

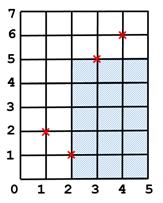
Explicație

O posibilă soluţie, de arie 15 se observă haşurată în desenul alăturat. Soluţia nu este unică, dar nu există o altă soluţie de arie mai mare.