Cerința
Se desenează un șir de pătrate distincte, de latură: 1,2,3,4,….
Pătratele sunt numerotate cu numerele egale cu laturile lor. Fiecare pătrat este împărțit în pătrate elementare, adică pătrate de latură 1. De exemplu, un pătrat de latură k se împarte, trasând k-1 linii orizontale și k-1 linii verticale echidistante, în k*k pătrate elementare dispuse căte k pe fiecare rând, respectiv coloană. Începând de la primul pătrat desenat, parcurgând în spirală fiecare pătrat din șir, se numerotează toate pătratele elementare, ca în imaginea de mai jos:
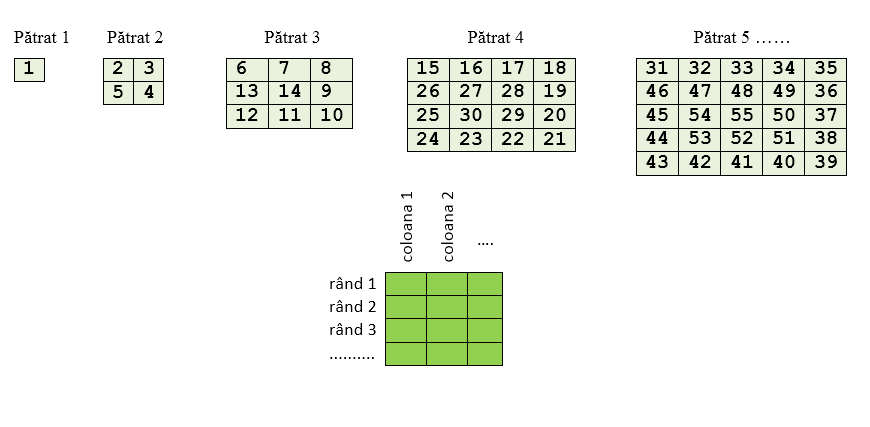
În fiecare pătrat din șir, rândurile sunt numerotate de sus în jos cu numerele distincte 1,2,3…. Analog, coloanele sunt numerotate de la stânga la dreapta cu numerele distincte 1,2,3….
Dându-se un număr natural N să se determine:
1) Numărul P al pătratului din șir care conține pătratul elementar numerotat cu N;
2) Rândul R și coloana C în care este situat pătratul elementar cu numărul N în pătratul cu numărul P.
Date de intrare
Fișierul de intrare npe.in conține pe prima linie numărul N.
Date de ieșire
Fișierul de ieșire npe.out va conține pe prima linie cele trei numere naturale P R C determinate, separate prin câte un spațiu, cu semnificația din enunț.
Restricții și precizări
1 ≤ N ≤ 2.000.000.000- Pentru determinarea corectă a numărului
Pse acordă40%din punctaj; pentru determinarea corectă a număruluiRse acordă30%din punctaj; pentru determinarea corectă a număruluiCse acordă30%din punctaj
Exemplu:
npe.in
52
npe.out
5 4 3
Explicație
Pătratul cu numărul P=5 conține pe rândul R=4 și coloana C=3 pătratul elementar cu numărul N=52.