Vrăjitorul Arpsod e prea supărat că arhitectul Ierdnac i-a furat inspiraţia, astfel ca nu poate să compună o poveste bună, deci va fi scurt şi la obiect: Dându-se o matrice de N x M cu valori întregi, să se determine ‘*T*-ul’ de sumă maximă şi numărul acestora.
Definim un T astfel:
1. Este format din două “linii” perpendiculare
2. Ambele “linii” sunt formate din cel puţin 3 căsuţe ( căsuţa de intersecţie se consideră comună )
3. Intersecţia celor două linii NU se face în capete ( exemplele 1, 3 şi 4 de la GREŞITE )
4. Pot fi rotite cu 0o, 90o, 180o sau 270o
Exemple de *T*-uri:
| T-uri CORECTE |
 |
| T-uri GREŞITE |
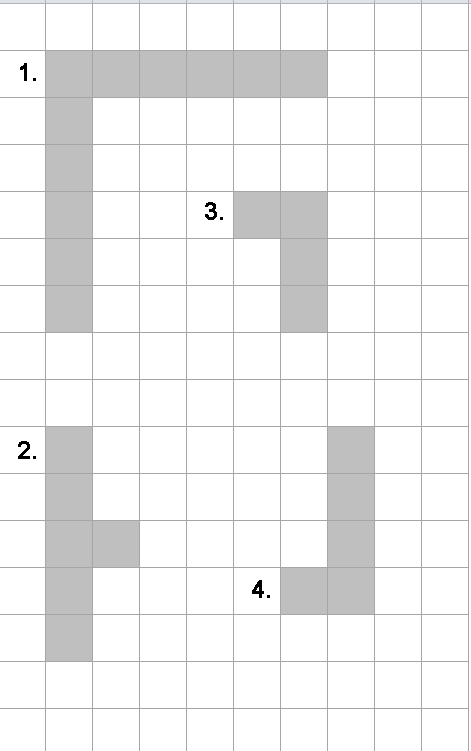 |
Cerința
Aflaţi suma maximă a unui ‘T’ şi numărul ‘T’-urilor de sumă maximă.
Date de intrare
Pe prima linie a fișierului tmax.in se află numerele naturale: N și M, reprezentând dimensiunile matricei. Urmeaza apoi câte N linii a câte M numere reprezentând elementele matricei.
Date de ieșire
Fișierul tmax.out va conţine, pe prima linie, separate prin spaţiu în această ordine suma maximă a unui T şi numărul acestora.
Restricții și precizări
6 < = N, M <= 1.000- Elementele matricei aparţin intervalului [
-2*109,2*109] - Două ‘T-uri’ se consideră distincte dacă există măcar o casuţă ce este conţinută de unul şi NU este conţinută de celălalt
- Veţi primi
70%din punctaj pe testul respectiv pentru determinarea corectă a primei valori şi30%pentru determinarea corectă a celei de-a doua valori - Pentru
30%din teste se garantează că10 <= N, M <= 300 - Fișierul de ieșire TREBUIE să conțină DOUĂ valori chiar dacă doriți să rezolvați o singură cerință din cele două
Exemplu:
tmax.in
6 6 -3 -7 1 -9 -8 -7 -1 -2 3 -2 -1 -5 -3 -4 1 -4 -4 -4 1 1 3 4 1 1 -5 -6 1 -3 -9 -4 -1 -2 1 -6 -8 -8
tmax.out
16 2
Explicație
| -3 | -7 | 1 | -9 | -8 | -7 | -3 | -7 | 1 | -9 | -8 | -7 | ||||
| 1 | -2 | 3 | -2 | -1 | -5 | 1 | -2 | 3 | -2 | -1 | -5 | ||||
| -3 | -4 | 1 | -4 | -4 | -4 | -3 | -4 | 1 | -4 | -4 | -4 | ||||
| 1 | 1 | 3 | 4 | 1 | 1 | 1 | 1 | 3 | 4 | 1 | 1 | ||||
| -5 | -6 | 1 | -3 | -9 | -4 | -5 | -6 | 1 | -3 | -9 | -4 | ||||
| -1 | -2 | 1 | -6 | -8 | -8 | -1 | -2 | 1 | -6 | -8 | -8 |