Acest site foloseşte cookies. Navigând în continuare, vă exprimaţi acordul asupra folosirii cookie-urilor.
Detalii evaluare #54109811
Rezumat problemă
#4288
Veverita5
În parcul orașului există 5 rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C, D și E, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:
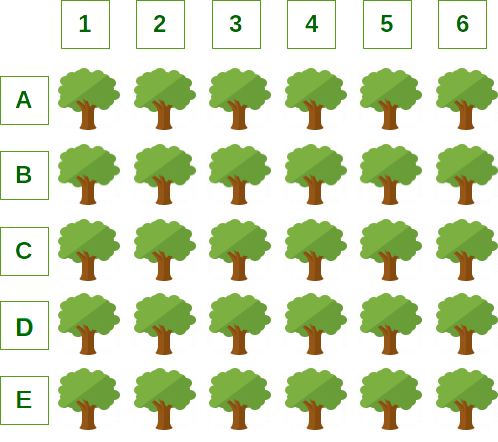
O veveriță jucăușă sare prin copaci astfel:
- pornește dintr-un copac numerotat cu
1; - la fiecare pas sare dintr-un copac numerotat cu
iîntr-un copac numerotat cui+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul E, va sări în copacul de pe rândul D, dacă se află în copacul de pe rândul B, va sări în copacul de pe rândul A sau în copacul de pe rândul C, dacă se află în copacul de pe rândul C, va sări în copacul de pe rândul B sau în copacul de pe rândul D,iar dacă se află în copacul de pe rândul D, va sări în copacul de pe rândul C sau în copacul de pe rândul E; - se oprește într-unul dintre copacii numerotați cu
n.
Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.
- Fișiere
- medie
Detalii
| Problema | Veverita5 | Operații I/O |

veverita5.in/veverita5.out
|
|---|---|---|---|
| Limita timp | 0.1 secunde | Limita memorie |
Total: 64 MB
/
Stivă 8 MB
|
| Id soluție | #54109811 | Utilizator | |
| Fișier | veverita5.cpp | Dimensiune | 2.11 KB |
| Data încărcării | 19 Noiembrie 2024, 22:18 | Scor / rezultat | 90 puncte |
Evaluare
Mesaj compilare
Rezultat evaluare
| Test | Timp | Mesaj evaluare | Scor posibil | Scor obținut | ||
|---|---|---|---|---|---|---|
| 1 | 0 secunde | OK. | 5 | 5 | Exemplu | |
| 2 | 0 secunde | OK. | 5 | 5 | ||
| 3 | 0 secunde | OK. | 5 | 5 | ||
| 4 | 0 secunde | Raspuns gresit. | 5 | 0 | ||
| 5 | 0 secunde | Raspuns gresit. | 5 | 0 | ||
| 6 | 0 secunde | OK. | 5 | 5 | ||
| 7 | 0 secunde | OK. | 10 | 10 | ||
| 9 | 0 secunde | OK. | 10 | 10 | ||
| 12 | 0 secunde | OK. | 10 | 10 | ||
| 13 | 0 secunde | OK. | 10 | 10 | ||
| 14 | 0 secunde | OK. | 10 | 10 | ||
| 15 | 0 secunde | OK. | 10 | 10 | ||
| 16 | 0 secunde | OK. | 10 | 10 | ||
| Punctaj total | 90 | |||||
Cum funcționează evaluarea?
www.pbinfo.ro permite evaluarea a două tipuri de probleme:
- probleme la care rezolvarea presupune scrierea unui program complet
- probleme la care rezolvarea presupune scrierea unei secvențe de program - câteva instrucțiuni, o listă de declarații, una sau mai multe funcții, etc.
Problema Veverita5 face parte din prima categorie. Soluția propusă de tine va fi evaluată astfel:
- Programul sursă este compilat folosind compilatorul corespunzător. Dacă în urma compilării se obțin erori sau avertismente, acestea sunt afișate în această pagină.
- Dacă programul a fost compilat, executabilul obținut va fi rulat, furnizându-i-se unul sau mai multe seturi de date de intrare, în concordanță cu restricțiile specifice problemei. Pentru fiecare set de date se obține un anumit punctaj, în raport cu corectitudinea soluției tale.
Suma punctajelor acordate pe testele utilizate pentru verificare este 100. Astfel, soluția ta poate obține cel mult 100 de puncte, caz în care se poate considera corectă.