Articole recomandate
Stars and bars
Stars and bars (Stele și bare) este o metodă de rezolvare a unor probleme de combinatorică. Se poate folosi când trebuie să determinăm numărul de modalități de a grupa un număr dat de obiecte identice.
Teoremă: Numărul de a variante de a plasa n obiecte identice în k cutii este egal cu: \( C_{n+k-1}^{k-1} \).
Demonstrația implică separarea celor n obiecte (stele) în k cutii prin k-1 bare – de unde și numele. De exemplu, configurația următoare are n=7 stele și k=4 cutii: \( \star \vert \star \star \vert \vert \star \star \star \star \) și corespunde următoarei situații:
- prima cutie conține un obiect
- a doua cutie conține două obiecte
- a treia cutie nu conține niciun obiect
- a patra cutie conține patru obiecte
Configurația este echivalentă cu următoarea configurație de biți: 0100110000, în care bitul 1 corespunde obiectului, \( \star \), iar 1 corespunde barei, \( \vert \). Toate configurațiile convenabile au n-k+1 biți, dintre care n au valoarea 0 și k-1 au valoarea 1 și corespund submulțimilor cu k-1 elemente ale unei mulțimi cu n+k-1 elemente.
Astfel, numărul lor este \( C_{n+k-1}^{k-1} \).
Consecință Ecuația \(x_1 + x_2 + x_3 + \cdots + x_k = n\) are \( C_{n+k-1}^{k-1} \) soluții întregi nenegative (mai mari sau egale cu 0).
Afirmația este echivalentă cu teorema de mai sus, în care \(x_i\) fiind egal cu numărul de obiecte din cutia i.
Teoremă: Numărul de a variante de a plasa n obiecte identice în k cutii astfel încât fiecare cutie conține cel puțin un obiect este egal cu: \( C_{n-1}^{k-1} \).
Demonstrația 1: Fixăm în fiecare cutie câte un obiect. Rămân \(n – k\) obiecte care trebuie plasate în \(k\) cutii, în condițiile teoremei de mai sus. Astfel, numărul de variante este \( C_{n-k+k-1}^{k-1} = C_{n-1}^{k-1} \).
Demonstrația 2: Folosim metoda Stars and bars. Separarea obiectelor în cutii se face plasând \(k\) bare în golurile dintre obiecte. Sunt \(n-1\) goluri în care putem plasa \(k\) bare în \( C_{n-1}^{k-1} \) moduri.
C++ STL bitset
bitset este un container special din STL care permite lucrul cu șiruri de biți. Aceștia sunt memorați eficient, pentru un bit din șir folosindu-se un bit în memorie. Astfel, spațiul de memorie ocupat de un bitset cu M biți este mai mic decât un tablou bool V[M]; sau un vector cu elemente de tip bool, dar numărul de biți M din bitset trebuie să fie cunoscut în momentul compilării, deci trebuie să fie o contantă.
Pot fi folosiți de exemplu pe post de vectori caracteristici, dar suportă și operațiile pe biți cunoscute pentru tipurile întregi.
Declararea
Pentru a folosi containerul bitset trebuie inclus headerul bitset:
#include <bitset>
Declararea se face astfel:
const int M = 16; bitset<M> B = 30;
Operații elementare
Afișarea
const int M = 16; bitset<M> B = 30; cout << B << endl;
Observații:
Meste constantă. Lipsa modificatoruluiconstduce la o eroare de compilare.- Când afișăm bitsetul, se afișează toți cei
Mbiți.
Indexarea
Biții din bitset sunt indexați de la 0 și pot fi accesați prin operatorul []. Bitul cel mai nesemnificativ (cel mai din dreapta) este B[0], iar bitul cel mai semnificativ este B[M-1], unde M este dimensiunea bitsetului.
const int M = 16; bitset<M> B = 30; // 0000000000011110 B[6] = 1; cout << B; // 0000000001011110
Compararea
Două containere bitset de aceeași dimensiune pot fi comparate cu operatorii == și !=.
Notă: operația != este eliminată în C++20.
Atribuirea
Putem să-i atribuim unui bitset valoarea unui întreg sau valoarea unui alt bitset. Prin atribuirea unui întreg, biții din bitsetul B devin identici cu biții din reprezentarea în memorie a valorii întregi care se atribuie:
const int M = 16; bitset<M> B, A; B = -30; cout << B << endl; // 1111111111100010 B = 5; cout << B << endl; // 0000000000000101 A = B; cout << A << endl; // 0000000000000101
Manipularea biților
Numărarea bitilor setați, numărul total de biți
Pentru a afle câți biți din bitset sunt setați (au valoarea 1), folosim metoda count(). Pentru a determina numărul total de biți, folosim metoda size(). Numărul biților nesetați (cu valoarea 0), facem diferența celor două.
const int M = 16; bitset<M> B = 63; cout << B.count() << endl; // 6 cout << B.size() << endl; // 16
Determinarea valorii unui bit
Se face cu metoda test(k), unde k reprezintă numărul de ordine al bitului dorit (de la dreapta spre stânga, incepând de la 0), iar rezultatul este 1 sau 0.
const int M = 16; bitset<M> B = 63; cout << B << endl; // 0000000000111111 cout << B.test(5) << endl; // 1 cout << B.test(6) << endl; // 0
Set, reset, flip
Bitsetul oferă metode pentru:
- setarea unui bit precizat:
B.set(k)dă valoarea1pentruB[k]B.set(k , r)dă valoarearpentruB[k]B.set()dă valoarea1pentru toți biții dinB
- resetarea unui bit precizat:
B.reset(k)dă valoarea0pentruB[k]B.reset()dă valoarea0pentru toți biții dinB
- schimbarea valoare biților (din
1devine0, iar din0devine1):B.flip(k)schimbă valoarea luiB[k]B.flip()schimbă valorile pentru toți biții dinB
bitset<M> B; B = 63; cout << B << endl; // 0000000000111111 //bitii se numeroteaza de la dreapta, incepand cu 0 B.reset(5); B.set(10); B.set(9 , 1); B.set(3 , 0); B.flip(2); cout << B << endl; // 0000011000010011 B.flip(); cout << B << endl; // 1111100111101100 B.set(); cout << B << endl; // 1111111111111111 B.reset(); cout << B << endl; // 0000000000000000
Operații pe biți
Operatii logice pe biți
Clasa bitset suportă operatorii logici pe biți (~, &, |, ^).
bitset<M> B, A; B = -60; A = 5; cout << "A = " << A << endl; // 0000000000000101 cout << "B = " << B << endl; // 1111111111000100 cout << "~B = " << ~B << endl; // 0000000000111011 cout << "A & B = " << (A & B) << endl; // 0000000000000100 cout << "A | B = " << (A | B) << endl; // 1111111111000101 cout << "A ^ B = " << (A ^ B) << endl; // 1111111111000001
Operatorii de deplasare
Clasa bitset suportă operatorii de deplasare a biților (<<, >>).
bitset<M> B; int n = 4; B = 7; cout << "B = " << B << endl; // 0000000000000111 cout << "B << n = " << (B << n) << endl; // 0000000001110000
Atribuiri
Clasa bitset suportă atriburile scurte: &=, |=, ^=, precum și <<=, >>=.
Fie A , B două containere bitset de aceași dimensiune și n un întreg. Atunci:
A &= Beste echivalent cuA = A & B;A |= Beste echivalent cuA = A | B;A ^= Beste echivalent cuA = A ^ B;A <<= neste echivalent cuA = A << n;A >>= neste echivalent cuA = A >> n;
Conversii
Bitset-ul poate fi convertit la
- string –
to_stringB.to_string()– returnează un string conținând reprezentarea binară a luiB, formată formată din caractere0și1;B.to_string(c0)– returnează un string conținând reprezentarea binară a luiB, caracterele0fiind înlocuite cu caracterulc0;B.to_string(c0 , c1)– returnează un string conținând reprezentarea binară a luiB, caracterele0și1fiind înlocuite cu caracterulc0, respectivc1;
- întreg fără semn-
to_ulong(),to_uulong()B.to_ulong()– retunează un întreg fără semn pe 32 de biți (unsingned int,unsigned long) cu reprezentarea binară echivalentă cu configurația bitsetuluiB;B.to_uulong()– retunează un întreg fără semn pe 64 de biți (unsigned long long) cu reprezentarea binară echivalentă cu configurația bitsetuluiB;- dacă valoarea întreagă corespunzătoare bitsetului nu poate fi reprezentată pe 32, respectiv 64 de biți, se va ridica o excepție de tip
overflow_error.
C++ vector - scurt tutorial
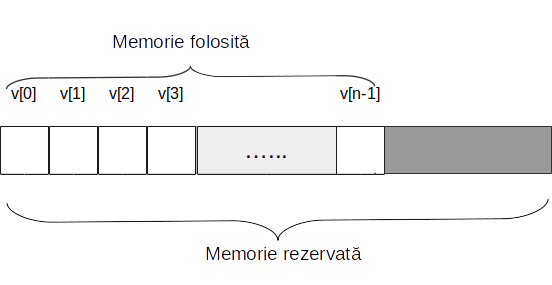
Containerul C++ vector este, probabil, cel mai folosit container STL. Vectorii sunt tablouri dinamice cu elemente omogene care au proprietatea de a se redimensiona automat când se adaugă sau se șterge un element, gestionarea memoriei fiind realizată automat de către container.
Vectorii sunt stocați într-o zonă contiguă de memorie și pot fi traversați cu ajutorul iteratorilor. Elementele se adaugă, de regulă la sfârșit. Operația de adăugare ia, de regulă, timp constant, cu excepția cazului când spatiul de memorie alocat trebuie redimensionat (mărit). Ștergerea unui element ia întotdeauna timp constant. Inserarea și ștergerea la începutul sau în interiorul vectorului iau timp liniar.
Declararea unui vector
Trebuie inclus header-ul vector:
#include <vector>;
Declararea se face astfel:
vector<T> V;
unde T este un tip de date. Acesta va fi tipul elementelor vectorului. Vectorul declarat mai sus este vid – are 0 elemente.
Alternativ, putem declara vectorul astfel:
vector<T> V(n);
n este un întreg. Se va crea un crea un vector V cu n elemente. Valorile acestora sunt valorile implicite pentru datele de tip T. Pentru tipurile numerice, valoarea elementelor este 0.
vector<T> V(n, vT);
n este un întreg, iar vT este o dată de tip T. Se va crea un crea un vector V cu n elemente. Valorile acestora sunt copii ale lui vT.
De exemplu:
vector<int> A; // se crează un vector A cu zero elemente cin >> n; vector<int> B(n); // se crează un vector B cu n elemente, egale cu 0 cin >> x; vector<int> C(n , x); // se crează un vector B cu n elemente, egale cu x
Atribuirea
Spre deosebire de tablourile standard C, vectorilor li se pot atribui valori în orice moment. Exemplu:
vector<int> A , B = {2 , 4, 6 , 8};
A = B;
A = {1 , 2 , 3 , 4 , 5};
Dimensiunea și capacitatea
Numărul de elemente din vector poate fi determinat cu funcția size():
vector<int> A = {2 , 4 , 6 , 8};
cout << A.size(); // 4
De regulă, memoria alocată pentru un vector este mai mare decât memoria folosită. Acest lucru se întâmplă pentru a se evita realocarea memoriei (operație costisitoare, care presupune copierea tuturor elementelor) de fiecare dată când se adaugă elemente.
Funcția capacity() returnează numărul de elemnte pe care le poate avea vectorul la momentul curent, fără a se realoca memoria. Are loc relația capacity() >= size(), iar numărul de elemente care pot fi adăugate fără realocare este capacity() - size().
Redimensionarea
Funcția resize() permite redimensionarea unui vector și are următoarele forme:
V.resize(n);(1)V.resize(n , x);(2)
Vectorul V se redimensionează încât să aibă n elemente:
- dacă
n < V.size(), în vector vor rămâne primelenelemente, celelalte vor fi șterse. - dacă
n > V.size(), în vector se vor adăugan - V.size()elemente egale cux, în cazul (2) sau egale cu valoarea implicită pentru tipul elementelor din vector, în cazul (1). Această valoare este0pentru tipurile numerice.
Adăugarea unui element
Adăugarea unui nou element în vector se face la sfârșit, cu funcția push_back():
vector<int> A; for(int i = 1 ; i <= 5 ; i ++) A.push_back(2 * i); cout << A.size();
Accesarea unui element
Elementele vectorilor pot fi accesate prin intermediul indicilor, cu operatorul []. Acesta nu verifică existență elementului cu un anumit indice, iar dacă acesta nu există, comportamentul programului este impredictibil.
vector<int> A; for(int i = 1 ; i <= 5 ; i ++) A.push_back(2 * i); for(int i = 0 ; i < A.size() ; i ++) cout << A[i] << ' '; // 0 2 4 6 8
De asemenea, este posibilă accesarea elementelor prin intermediul funcției at(). Aceasta returnează o referință la elementul de la poziția dată, iar dacă acesta nu există ridică o excepție care poate fi capturată prin mecanismul try … catch.
vector<int> A = {2 , 4 , 6 , 8 , 10};
A.at(1) = 20; //A = {2 , 20 , 6 , 8 , 10}
for(auto x : A)
cout << x << " ";
Primul și ultimul element poate fi accesat prin intemediul funcțiilor front() și back(). Ele returnează referințe la primul, respectiv ultimul element al vectorului. Comportamentul este impredictibil dacă vectorul este vid.
vector<int> A = {2 , 4 , 6 , 8 , 10};
A.at(1) = 20; //A = {2 , 20 , 6 , 8 , 10}
A.front() = 7; //A = {7 , 20 , 6 , 8 , 10}
A.back() = 5; //A = {7 , 20 , 6 , 8 , 5}
for(auto x : A)
cout << x << " ";
Iteratori
Iteratorii sunt similari cu pointerii. Cu ajutorul lor putem identifica adresa elementelor din vector. Iteratorii pot fi dereferențiați (obtinând referințe la elemente), pot fi incrementați/decrementați și pot fi adunați cu scalari.
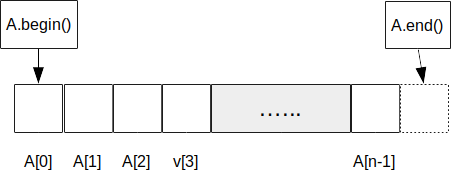
Vectorii oferă prin intermediul funcției begin() un iterator la primul element al funcției, iar prin end() un iterator la elementul de după ultimul element al vectorului.
vector<int> A = {2 , 4 , 6 , 8 , 10};
vector<int>::iterator I;
for(I = A.begin() ; I < A.end() ; I ++)
cout << *I << " "; // 2 4 6 8 10
Observații:
- tipul variabilei iterator trebuie să fie în concordanță cu tipul elementelor vectorului;
- pentru a lucra cu elementul pentru care cunoaștem iteratorul, acesta trebuie să fie dereferențiat:
*I; - rezultatul funcției
A.end()este un iterator, dar acestuia nu-i corespunde un element al vectorului. Valoarea sa este adresa de după ultimul element al vectorului.
Clasa vector conține și funcțiile rbegin() și rend(), care returnează iteratori de tip reverse iterator, care permit parcurgerea vectorului în ordien inversă:
vector<int> A = {2 , 4 , 6 , 8 , 10};
for(vector<int>::reverse_iterator I = A.rbegin() ; I < A.rend() ; I ++)
cout << *I << " ";
Acești iteratori fac parte din categoria iteratorilor cu acces aleatoriu. Este cea mai puternică categorie de iteratori (cu cele mai multe operații definite). Aceste operații sunt:
| Expresie | Rezultat, efect |
|---|---|
*I |
Dereferențiere |
I->camp |
Acces la câmpurile structurii/membrii clasei memorate în elementele vectorului |
++I |
Preincrementare. Rezultatul este poziția următoare |
I++ |
Postincrementare. Rezultatul este poziția inițială |
--I |
Predecrementare. Rezultatul este poziția anterioară |
I-- |
Postdecrementare. Rezultatul este poziția inițială |
I == J |
Egalitate între doi iteratori |
I != J |
Neegalitate între doi iteratori |
<, >, <=, >= |
Operatori relaționali. Operanzii sunt iteratorii. Rezultatul este conform cu poziția în vector a elementelor adresate de cei doi iteratori |
I[k] |
Elementul de pe poziția k, începând de la I |
I += k |
k pași înainte |
I -= k |
k pași înapoi |
I + k |
iterator spre al k-lea element după cel curent |
I - k |
iterator spre al k-lea element înaintea celui curent |
I - J |
distanța în vector între iteratorii I și J |
Parcurgerea unui vector
O primă modalitate de parcurgere este folosind indicii, similar cu parcurgerea tablourilor standard C. Pentru determinarea numărului de elemnte există functia size():
vector<int> A = {2 , 4 , 6 , 8 , 10};
for(int i = 0 ; i < A.size(); i ++)
cout << A[i] << " ";
De asemenea, putem folosi iteratorii:
vector<int> A = {2 , 4 , 6 , 8 , 10};
for(vector<int>::iterator I = A.begin() ; I < A.end() ; I ++)
cout << *I << " ";
Pentru ușurință, putem folosi specificatorul de tip auto pentru a stabili tipul iteratorului:
vector<int> A = {2 , 4 , 6 , 8 , 10};
for(auto I = A.begin() ; I < A.end() ; I ++)
cout << *I << " ";
Începând de la versiunea 2011 a standardului C++ există o formă specială a instrucțiunii for, care permite parcurgerea elementelor unui container:
vector<int> A = {2 , 4 , 6 , 8 , 10};
for(int x : A)
cout << x << " ";
Specificatorul de tip auto poate fi folosit și aici. În secvența de mai sus, x reprezintă pe rând câte o copie a elementelor din A. Eventualele modificări ale lui x nu vor modifica valorile elementelor din A. Dacă se dorește modificare elemenelor din A, atunci x trebuie să fie o referință:
vector<int> A = {2 , 4 , 6 , 8 , 10};
for(int & x : A)
x *= 2;
for(int x : A)
cout << x << " ";
Parcurgerea inversă
Vectorii suportă iteratori reversibili, care permit parcurgerea containerului în ordine inversă. Clasa vector are metodele:
rbegin()– returnează un iterator reversibil la ultimul element din containerrend()– returnează un iterator reversibil la elementul din fața primului
Parcurgerea se poate face astfel:
for(vector<int>::reverse_iterator I = V.rbegin() ; I < V.rend() ; I ++) cout << *I << " ";
Inserarea elementelor
Pentru adăugarea la sfârșit se folosește metoda push_back(). Pentru inserarea de noi elemente în interiorul containerului se folosește metoda insert(), care are mai multe forme:
V.insert(pos , x)– inserează în vectorulV, în fața iteratoruluiposun nou element cu valoareax;V.insert(pos , cnt , x)inserează în vectorulV, în fața iteratoruluipos,cntnoi elemente egale cux;V.insert(pos , st , dr)inserează în vectorulV, în fața iteratoruluipos,dr-stnoi elemente, având valorile egale cu cele ale elementelor din secvența[st, dr)dintr-un container oarecare. Dacă vectorulVși secvența[st,dr)se suprapun rezultatul este impredictibil.
Rezultatul apelurilor de mai sus este un iterator la primul element inserat.
Apelurile de mai sus invalidează toți iteratorii și referințele la elemente din V, dacă în urma inserării se realocă memorie, respectiv se invalidează iteratorii și referințele din dreapta lui pos, în caz contrar.
Mai multe detalii despre insert() aici: https://en.cppreference.com/w/cpp/container/vector/insert.
Eliminarea elementelor
Pentru eliminarea tuturor elementelor intr-un vector există metoda clear().
V.clear();
În urma eliminării, rezultatul lui V.size() este 0.
Pentru eliminarea ultimului element al tabloului există metoda pop_back(). În urma apelului se invalidează iteratorii și referințele la ultimul element, precum și iteratorul end().
Pentru eliminarea unor elemente oarecare se folosește metoda erase(), cu următoarele forme:
V.erase(pos)– elimină elementul indicat de iteratorulpos.posnu poate fi egal cuend()V.erase(st , dr)– elimină elementele din intervalul[st,dr), undestșidrsunt iteratori la elemente dinV
Rezultatul funcției erase() este un iterator la elementul de după ultimul element eliminat.
Se invalidează iteratorii și iteratorii din dreapta lui posm inclusiv iteratorul end().
Mai multe detalii aici: https://en.cppreference.com/w/cpp/container/vector/erase.
STL - Concepte fundamentale
Standard Template Library reprezintă un ansamblu de mecanisme scrise în C++ pentru gestionarea eficientă a unor colecții de date, împreună cu algoritmi eficienți care prelucrează aceste date. Este parte a Bibliotecii Standard C++, fiind astfel disponibilă în orice compilator care respectă standardul C++.
Introducere
STL are trei componente fundamentale: containerele, iteratorii și algoritmii, precum și o serie de componente suplimentare: containerele speciale, functorii, alocatorii.
Containerele
Containerele sunt obiecte care conțin date (de orice tip, putând fi la rândul containere). Alocarea memoriei pentru conținutul containerelor se face automat (de regulă dinamic), de către container.
Containerele sunt de două tipuri: containere secvențiale și containere asociative.
Containerele secvețiale gestionează un ansamblu de elemente dispuse strict liniar. Fiecare element al containerului are o poziție bine stabilită, care nu depinde de valoarea elementului. Avem următoarele contaniere secvențiale:
- vector – gestionează o secvență de elemente asemănătoare tablourilor standard C;
- deque (double-ended queue)- este o coadă cu operații rapide de adăugare și eliminare la ambele capete;
- list – gestionează o listă alocată dinamic, oferind operațiile de bază cu aceasta.
Timpul necesar pentru operațiile uzuale asupra containerelor secvențiale este redat mai jos:
| Operație | vector | deque | list |
|---|---|---|---|
| Accesarea primului element | constant | constant | constant |
| Accesarea ultimului element | constant | constant | constant |
| Accesarea unui element oarecare | constant | constant | liniar |
| Adăugare/ștergere la început | liniar | constant | constant |
| Adăugare/ștergere la sfârșit | constant | constant | constant |
| Adăugare/ștergere oarecare | liniar | liniar | constant |
Containerele asociative sunt structuri de date în care fiecare element are asociată o anumită cheie și are o anumită valoare. Ordinea elementelor în container depinde de cheie și se poate schimba în funcție de celelalte elemente. Aceste containere implementează eficient operațiile de adăugare de noi elemente, ștergere a elementelor în funcție de cheie, precum și căutarea elementelor după cheie.
Sunt două familii de containere asociative:
- set – în care cheia și valoarea elementelor sunt identice; containerele de acest tip sunt:
- set – memorează elemente distincte; elementele sunt menținute în ordine (strict) crescătoare;
- multiset – elementele pot fi egale și sunt menținute în ordine crescătoare;
- unordered_set – memorează elemente distincte; nu este garantată o anumită ordine a elementelor;
- unordered_multiset – elementele pot fi egale și nu este garantată o anumită ordine a elementelor
- map – cheile și valorile diferă; accesul la elemente se face prin intermediul cheii; containerele de acest tip sunt:
- map – cheile sunt distincte; elementele sunt menținute în ordine (strict) crescătoare a cheilor;
- multimap – cheile pot fi egale și sunt menținute în ordinea crescătoare a cheilor;
- unordered_map – cheile sunt distincte; nu este garantată o anumită ordine a elementelor;
- unordered_map – cheile pot fi egale și nu este garantată o anumită ordine a elementelor.
Timpii necesari pentru operațiile de adăugare, ștergere și acces sunt logaritmici pentru containerele asociative care menține elementele ordonate și constanți pentru containerele care nu mențin elementele în ordine.
Iteratorii
Iteratorii reprezintă o generalizare a conceputului de pointer. Ei oferă acces la elementele containerelor într-o manieră uniformă, pentru toate containere și pentru toți algoritmii STL.
Operațiile cu iteratorii sunt similare cu operațiile cu pointeri, putându-i dereferenția, incrementa/decrementa, compara, aduna cu întreg, etc. Unele operații sunt disponibile pentru toți iteratorii, altele doar pentru cei ai unor anumite tipuri de container.
Algoritmii
Algoritmii prelucrează colecții de elemente. Aceste colecții pot fi containere, părți ale unor containere sau slte structuri de date care permit lucrul cu pointeri (de exemplu tablouri standard C).
Algoritmii sunt folosiți sub formă de funcții, iar prelucrările pe care le fac sunt diverse: sortări, căutări, modificări, etc.
Containere speciale
Containerele speciale sunt:
- bitset – folosit pentru manipularea eficientă a șirurilor de biți
- containere adaptor – acoperă necesități speciale și sunt create pornind de la containere standard: containerele stack și queue permit gestionarea ușoară a unei stive, respectiv a unei cozi și sunt create pe baza containerului deque, iar containerul priority_queue gestionează o coadă de priorități (heap) și este creat pe baza clasei vector.
Functori și alocatori
Functorii sunt obiecte care se folosesc în maniera unui apel de funcție. Sunt folosite frecvent în cadrul algoritmilor.
Alocatorii sunt obiecte care gestionează alocarea memoriei pentru orice obiect și, în particular, pentru obiectele care fac parte dintr-un container.
Operații logice
Operațiile logice lucrează cu valori de adevăr. Le folosim instinctiv în viața de zi cu zi, dar uneori ne pun în dificultate atunci când trebuie să le aplicăm într-un algoritm.
Valori de adevăr. Propoziții adevărate și false
Operațiile logice se fac cu valori de adevăr (notate TRUE / FALSE, sau ADEVĂRAT / FALS) sau propoziții care au ca rezultat valori de adevăr. De exemplu:
- “Orașul Sibiu este în România.” – este o propoziție adevărată, are valoarea
ADEVĂRAT; - “Orașul Sibiu este în Bulgaria.” – este o propoziție falsă, are valoare
FALS.
Exemple din matematică:
- numărul
19este impar –ADEVĂRAT 10se divide cu3–FALS- comparații:
3 ≠ 4–ADEVĂRAT10 < 5–FALSx > 3– nu știm rezultatul; depinde de valoarea luix!!
Exemple din algoritmică (C/C++):
19%2==1–ADEVĂRAT, în C/C++ rezultatul este110%3==0–FALS, în C/C++ rezultatul este03 != 4–ADEVĂRAT, în C/C++ rezultatul este110 < 5–FALS, în C/C++ rezultatul este0x > 3– nu știm rezultatul; depinde de valoarea luixdin momentul in care se face comparația!!
De multe ori o propoziție logică conține variabile, iar valoarea de adevăr a ei depinde de valorile variabilelor.
Două propoziții logice, care depind de anumite variabile, sunt echivalente dacă, pentru orice valori ale variabilelor, sunt fie amândouă adevărate, fie amândouă false. De exemplu, propoziția “numărul natural n este par” este echivalentă cu propoziția “restul împărțirii numărului natural n la 2 este 0”.
Operațiile logice
Negarea
Negarea este o operație foarte folosită în viața de zi cu zi. Prin negare, propoziția “Orașul Sibiu este în România.” devine “Orașul Sibiu nu este în România.”, care este FALSĂ. Prin negarea unei propoziții adevărate se obține o propoziție falsă, iar prin negarea unei propoziții false se obține o propoziție adevărată.
În C/C++, negarea este o operație unară, cu prioritate mare, iar operatorul său este !. Ea poate fi aplicată pentru orice valori numerice (și nu numai), dar de regulă se aplică asupra altor valori logice.
- dacă
peste o expresie cu valoarea0(FALS), atunci!pare valoarea1(ADEVĂRAT). - dacă
peste o expresie cu valoarea diferită de0(ADEVĂRAT), atunci!pare valoarea0(FALS).
Exemple:
int x = 10; cout << !(x == 10); // 0: x == 10 este adevărat și are rezultat 1, 1 negat este 0 cout << !x == 10; // tot 0, dar se efectuează mai întâi !x, adică !10, cu rezultat 0, apoi 0 == 10, cu rezultat fals, adică 0 cout << !(x < 5); // 1: x < 5 este fals, adică 0, 0 negat este 1
Conjuncția
Conjuncția realizează “compunerea” a două propoziții prin intermediul cuvântului ȘI. Exemple:
- Propoziția “Orașul Sibiu este în România.” ȘI “Orașul Craiova este în România.” este obținută prin compunerea a două propoziții adevărate și este la rândul său adevărată;
- Propoziția “Orașul Sibiu este în România.” ȘI “Orașul Craiova este în Bulgaria.” este obținută prin compunerea unei propoziții adevărate cu una falsă și este la rândul său falsă;
- Propoziția “Orașul Sibiu este în Bulgaria.” ȘI “Orașul Craiova este în România.” este obținută prin compunerea unei propoziții false cu una adevărate și este la rândul său falsă;
- Propoziția “Orașul Sibiu este în Bulgaria.” ȘI “Orașul Craiova este în Bulgaria.” este obținută prin compunerea a două propoziții false și este la rândul său falsă.
Astfel, conjuncția a două propoziții este ADEVĂRAT dacă ambele propoziții sunt adevărate, în toate celelalte cazuri este FALSĂ.
În C/C++ simbolul conjuncției este &&. La fel ca negarea, și conjuncția poate fi aplicată pentru orice valori numerice (și nu numai), dar de regulă se aplică asupra altor valori logice.
Fie p și q două valori numerice:
- dacă
peste nenul șiqeste nenul, atunci(p&&q)==1; - dacă
peste nenul șiqeste nul, atunci(p&&q)==0; - dacă
peste nul șiqeste nenul, atunci(p&&q)==0; - dacă
peste nul șiqeste nul, atunci(p&&q)==0;
Exemple:
cout << (1 < 2 && 2 == 1 + 1); // 1; ADEVĂRAT ȘI ADEVĂRAT este ADEVĂRAT cout << (1 < 2 && 2 != 1 + 1); // 0; ADEVĂRAT ȘI FALS este FALS cout << (1 == 2 && 2 == 1 + 1); // 0; FALS ȘI ADEVĂRAT este FALS cout << (1 == 2 && 2 != 1 + 1); // 0; FALS ȘI FALS este FALS
Disjuncția
Conjuncția realizează “compunerea” a două propoziții prin intermediul cuvântului SAU. Exemple:
- Propoziția “Orașul Sibiu este în România.” SAU “Orașul Craiova este în România.” este obținută prin compunerea a două propoziții adevărate și este la rândul său adevărată;
- Propoziția “Orașul Sibiu este în România.” SAU “Orașul Craiova este în Bulgaria.” este obținută prin compunerea unei propoziții adevărate cu una falsă și este la rândul său adevărată;
- Propoziția “Orașul Sibiu este în Bulgaria.” SAU “Orașul Craiova este în România.” este obținută prin compunerea unei propoziții false cu una adevărate și este la rândul său adevărată;
- Propoziția “Orașul Sibiu este în Bulgaria.” SAU “Orașul Craiova este în Bulgaria.” este obținută prin compunerea a două propoziții false și este la rândul său falsă.
Astfel, disjuncția a două propoziții este ADEVĂRATĂ dacă cel puțin una dintre ele este adevărată; dacă ambele propoziții sunt false, disjucția lor este FALSĂ.
În C/C++ simbolul disjuncției este ||. La fel ca negarea și conjuncția, și disjuncția poate fi aplicată pentru orice valori numerice (și nu numai), dar de regulă se aplică asupra altor valori logice.
Fie p și q două valori numerice:
- dacă
peste nenul șiqeste nenul, atunci(p || q)==1; - dacă
peste nenul șiqeste nul, atunci(p || q)==1; - dacă
peste nul șiqeste nenul, atunci(p || q)==1; - dacă
peste nul șiqeste nul, atunci(p || q)==0;
Exemple:
cout << (1 < 2 || 2 == 1 + 1); // 1; ADEVĂRAT SAU ADEVĂRAT este ADEVĂRAT cout << (1 < 2 || 2 != 1 + 1); // 1; ADEVĂRAT SAU FALS este ADEVĂRAT cout << (1 == 2 || 2 == 1 + 1); // 1; FALS SAU ADEVĂRAT este ADEVĂRAT cout << (1 == 2 || 2 != 1 + 1); // 0; FALS SAU FALS este FALS
Exerciții
7 11 17 19 28 509
Legile lui De Morgan
Acestea stabilesc niște reguli legate de situația în care aplicăm operația de negare asupra unor conjuncții și disjuncții. Formal, ele se exprimă astfel:
Fie p și q două expresii logice. Atunci:
!(p && q) ↔ !p || !q!(p || q) ↔ !p && !q
Prin ↔ se înțelege echivalența a două propoziții.
Exemplu
Fie n un număr natural. Dorim o condiție care să fie adevărată dacă și numai dacă n are exact două cifre. Această condiție este: “mai mare sau egal cu 10 și mai mic decât 100”. Expresia C/C++ este: n >= 10 && n < 100.
Care este condița inversă? Adică, cum exprimăm faptul că n nu are exact două cifre? Dacă n nu are exact două cifre înseamnă că n are o cifră sau n are cel puțin trei cifre. Adică “este mai mic decât 10 sau mai mare sau egal cu 100”. În C/C++: n < 10 || n >= 100.
Adică !(n >= 10 && n < 100) este echivalent cu n < 10 || n >= 100.
Atenție: nu există nicio valoare pentru care n < 10 && n >= 100.
Exerciții
15 18 61 476 529
Subșir crescător de lungime maximă
n elemente, numere naturale. Determinați un cel mai lung subșir crescător al șirului.
De exemplu, pentru n=10 și șirul A=(5, 10, 7, 4, 5, 8, 9, 8, 10, 2), cel mai lung subșir crescător va conține 5 elemente (5, 7, 8, 9, 10) sau (4, 5, 8, 9, 10).
Problema este una clasică și se rezolvă prin programare dinamică. Subșirul cerut se mai numește și subșir crescător maximal.
O soluție \(O(n^2)\)
Determinarea lungimii maxime
Pentru a determina lungimea maximă a unui subșir crescător al lui A, vom construi un șir suplimentar LG[], cu proprietatea că LG[i] este lungimea maximă a unui subșir care se începe în A[i]. Atunci lungimea maximă a unui subșir crescător va fi cel mai mare element din tabloul LG.
Vom construi șirul LG progresiv, începând de la ultimul element din A, bazându-ne pe următoarele observații:
LG[i] ≥ 1,∀iLG[n] = 1- vom determina
LG[i]astfel: analizăm toate elementeleA[j], cuj>iși îl alegem pe acela pentru careLG[j]este maxim șiA[i]≤A[j]. Fiejmaxindicele acestui element. AtunciLG[i]devineLG[i] = LG[jmax] + 1– elementulA[i]se lipește de subșirul care începe înA[jmax].
Secvență C++:
LG[n] = 1;
for(int i = n - 1 ; i > 0 ; i --)
{
LG[i] = 1;
for(int j = i + 1 ; j <= n; ++ j)
if(A[i] <= A[j] && LG[i] < LG[j] + 1)
LG[i] = LG[j] + 1;
}
După construirea șirului LG, lungimea subșirului maximal se determină ca fiind cea mai mare valoare din tabloul LG.
int pmax = 1;
for(int i = 2 ; i <= n ; i ++)
if(LG[i] > LG[pmax])
pmax = p;
cout << LG[pmax];
Reconstituirea subșirului
Există mai multe modalități de reconstituire a subșirului maximal. De asemenea, trebuie spus că pot exista mai multe șiruri maximale; în unele probleme poate fi determinat oricare, în altele trebuie determinat un subșir cu proprietăți suplimentare.
O soluție constă în construirea unui șir suplimentar, Next cu următoarea semnificație: Next[i] este următorul element în subșirul crescător maximal care începe cu A[i]. Dacă nu există un element următor, atunci LG[i] = -1. Acest tabloul se construiește în același timp cu LG, astfel:
LG[n] = 1, Next[n] = -1;
for(int i = n - 1 ; i > 0 ; i --)
{
LG[i] = 1 , Next[n] = -1;
for(int j = i + 1 ; j <= n; ++ j)
if(A[i] <= A[j] && LG[i] < LG[j] + 1)
LG[i] = LG[j] + 1, Next[i] = j;
}
Pentru a afișa subșirul, vom extrage informațiile necesare din șirul Next, pornind de la indicele pmax determinat mai sus:
int p = pmax;
do
{
cout << p << " ";
p = Next[p];
}
while(p != -1);
Putem reconstitui subșirul fără a construi șirul Next. La fiecare pas al structurii repetitive de mai sus vom determina un indice pUrm cu proprietatea că LG[pUrm]==LG[p]-1 și A[p] ≤ A[pUrm]:
int p = pmax;
do
{
cout << p << " ";
int pUrm = p + 1;
while(pUrm <= n && ! (A[pUrm] >= A[p] && LG[pUrm] == LG[p] - 1))
pUrm ++;
if(pUrm <= n)
p = pUrm;
else
p = -1;
}
while(p != -1);
Altă soluție \(O(n^2)\)
Putem regândi algoritmul de mai sus, astfel încât LG[i] să reprezinte lungime a maximă a unui subșir maximal care se termină în A[i].
- evident,
LG[1]=1; - pentru fiecare element
A[i]din șirul dat, vom parcurge elementele din fața sa și îl vom alege peA[p]atfel încâtA[p]≤A[i]șiLG[p]este maxim. În acest caz,A[i]se adaugă la subșirul care se încheie înA[p], adicăLG[i]devineLG[p]+1.
Lungimea subșriului maximal este cea mai mare valoare din LG, iar recosntituirea lui se face asemănător cu metoda de mai sus, folosind un șir de predecesori Prev[], unde Prev[i] este elementul din fața lui A[i] în subșirul crescător maximal care se încheie în A[i].
O soluție \(O(n \cdot \log n)\)
Algoritmul de mai sus are complexitate pătratică. Următoarea idee permite obținerea unui algoritm \(O(n \cdot \log{n})\).
Vom construi șirul D[], unde D[j] reprezintă un element al șirului A în care se termină un subșir crescător maximal de lungime j. Numărul de elemente pe care le va avea la final tabloul D va reprezenta lungimea subșirului crescător maximal al întregului șir A.
Vom construi șirul D în felul următor:
- fie
klungimea șiruluiD. Inițializămk=1șiD[k]=A[1]; - parcurgem șirul
A, începând de la al doilea element:- dacă
A[i]≥D[k], îl adăugăm peA[i]în șirulD– subșirul crescător maximal al luiAcrește cu încă un element - dacă
A[i]<D[k], vom înlocui cuA[i]pe cel mai mai mic element dinDcare este mai mare decât acesta
- dacă
ATENȚIE: Șirul D[] nu conține un subșir crescător al șirului A[]!
Exemplu
Pentru A=(5, 10, 7, 4, 5, 8, 9, 8, 10, 2).
Inițial k=1; D[k]=5; parcurgem șirul A, începând de la al doilea element:
i |
A[i] |
Condiție | Acțiune | D[] |
| 1 | 5 | - | - | (5) |
| 2 | 10 | A[i]>=D[k] |
adăugare | (5, 10) |
| 3 | 7 | A[i]<D[k] |
înlocuire | (5, 7) |
| 4 | 4 | A[i]<D[k] |
înlocuire | (4, 7) |
| 5 | 5 | A[i]<D[k] |
înlocuire | (4, 5) |
| 6 | 8 | A[i]>=D[k] |
adăugare | (4, 5, 8) |
| 7 | 9 | A[i]>=D[k] |
adăugare | (4, 5, 8, 9) |
| 8 | 8 | A[i]<D[k] |
înlocuire | (4, 5, 8, 8) |
| 9 | 10 | A[i]>=D[k] |
adăugare | (4, 5, 8, 8, 10) |
| 10 | 2 | A[i]<D[k] |
înlocuire | (2, 5, 8, 8, 10) |
Observații
- valorile din șirul
Dsunt în ordine crescătoare - fiecare element din șirul
Amodifică exact un element din șirulD(prin adăugare sau înlocuire).
Aceste observații ne permit să folosim căutarea binară pentru a stabili elementul din D care va fi înlocuit la fiecare pas: vom căuta primul element din D care este mai mare decât A[i]. Acest lucru poate fi realizat manual sau folosind funcția STL upper_bound. Complexitatea va fi \(O(n \cdot \log k)\).
Secvență C++
k = 1, D[k] = A[1];
for(int i = 2 ; i <= n ; i ++)
{
if(A[i] >= D[k])
P[++k] = A[i];
else
{
int st = 1 , dr = k , poz = k + 1;
while(st <= dr)
{
int m = (st + dr) / 2;
if(D[m] > A[i])
poz = m , dr = m - 1;
else
st = m + 1;
}
D[poz] = A[i];
}
}
cout << k << endl;
Reconstituirea subșirului
Pentru a reconstitui sub șirul crescător maximal vom folosi încă un șir P[], unde P[i] reprezintă poziția în șirul D unde a fost plasat (prin adăugare sau prin înlocuire) A[i]. Acesta este construit, pas cu pas, odată cu șirul D[]. Dacă un element A[i] face parte din subșirul crescător maximal, atunci P[i] reprezintă poziția sa în subșir.
Pentru exemplul de mai sus, șirul P[] va fi la final (1,2,2,1,2,3,4,4,5,1).
Reconstituirea propriu-zisă a subșirului se face în felul următor:
- fie
k– lungimea subșirului crescător maximal; - căutăm în șirul
P[]un element egal cuk. FieIkpoziția sa. AtunciA[Ik]reprezintă ultimul element al subșirului crescător maximal – cel de pe pozițiak; - căutăm în șirul
P[]un element egal cuk-1, anterior elementului de indiceIk. FieIk-1poziția sa. - analog se caută în
P[]valorilek-2, k-3, ..., 2, 1. - subșirul crescător maximal va fi
(A[I1], A[I2], ..., A[Ik]).
Secvența C++
În secvența de mai jos șirul I[] construit va conține indicii elementelor din A[] care fac parte din subșirul comun maximal.
k = 1;
D[k] = A[1];
P[1] = 1;
for(int i = 2 ; i <= n ; i ++)
if(A[i] >= D[k])
D[++k] = A[i], P[i] = k;
else
{
int st = 1 , dr = k , p = k + 1;
while(st <= dr)
{
int m = (st + dr) / 2;
if(D[m] > A[i])
p = m, dr = m - 1;
else
st = m + 1;
}
D[p] = A[i];
P[i] = p;
}
int j = n;
for(int i = k ; i >= 1 ; i --)
{
while(P[j] != i)
j --;
I[i] = j;
}
Probleme propuse
Numărul de drumuri în matrice
Introducere
Considerăm o matrice (labirint, teren, etc.) cu n linii și m coloane și un mobil aflat inițial în elementul de coordonate (1,1) – colțul stânga-sus, care se poate deplasa din elementul curent, de coordonate (i,j) în unul dintre elementele de coordonate (i+1,j) – aflat pe linia următoare, și (i,j+1) – aflat pe următoarea coloană. Să se determine în câte moduri poate ajunge mobilul în elementul de coordonate (n,m) – colțul dreapta-jos.
Problema are cel puțin două soluții, una care folosește metoda programării dinamice și una care se bazează pe combinatorică.
Rezolvare cu programare dinamică
Să constatăm mai întâi că numărul de drumuri căutat depinde de n și m – la mintea cocoșului, am putea spune. În general, numărul de drumuri de la poziția (1,1) la poziția (i,j) depinde de i și j, și numai de acestea. Atunci, formula recursivă care calculează rezultatul pentru (i,j) va depinde numai de i și de j!
Ne propunem să determinăm numărul de modalități în care mobilul ajunge de la poziția (1,1) în poziția (i,j). Fie acest număr \(F_{i,j}\). Constăm următoarele:
- în orice element de pe linia
1se poate ajunge într-un singur mod, dinspre stânga, deoarece în poziția(1,j)se poate ajunge numai din poziția(1,j-1). Astfel, \(F_{1,j} = 1\). - în orice element de pe coloana
1se poate ajunge într-un singur mod, dinspre linia anterioară, deoarece în poziția(i,1)se poate ajunge numai din poziția(i-1,1). Astfel, \(F_{i,1} = 1\). - în poziția
(i,j)(cui>1șij>1) se poate ajunge în două moduri:- de sus, din poziția
(i-1,j); - din stânga, din poziția
(i,j-1);
- de sus, din poziția
- atunci numărul de posibilități de a ajunge în poziția
(i,j)este numărul de posibilități de a ajunge în poziția(i-1,j)adunat cu numărul de posibilități de a ajunge în poziția(i,j-1). Astfel, \(F_{i,j} = F_{i-1,j} + F_{i,j-1}\). - rezultatul este \(F_{n,m}\).
În concluzie:
\( F_{i,j} = \begin{cases}
1& \text{dacă } i = 1 \text{ sau } j = 1, \\
F_{i-1,j} + F_{i,j-1}& \text{ dacă } i > 1 \text{ și } j > 1
\end{cases} \)
Deoarece formulele se suprapun, implementarea recursivă este foarte lentă. În consecință vom folosi o structură de date suplimentară, mai precis un tablou bidimensional în care A[i][j] reprezintă numărul de modalități de a ajunge din poziția (1,1) în poziția (i,j).
Acest tablou poate fi construit în maniera bottom-up:
int n, m, A[NN][NN]; ... for(int i = 1 ; i <= n ; ++ i) A[i][1] = 1; for(int j = 1 ; j <= m ; ++ j) A[1][j] = 1; for(int i = 2 ; i <= n ; ++ i) for(int j = 2 ; j <= m ; ++ j) A[i][j] = (A[i-1][j] + A[i][j-1]) % 9901; cout << A[n][m];
De asemenea, recurența poate fi rezolvată în maniera top-down, cu memoizare:
int n, m, A[NN][NN];
int F(int i , int j)
{
if(A[i][j] != 0)
return A[i][j];
if(i == 1 || j == 1)
A[i][j] = 1;
else
A[i][j] = (F(i-1,j) + F(i,j-1)) % 9901;
return A[i][j];
}
...
cout << F(n,m);
Rezolvare folosind calcul combinatorial
Pentru această soluție, să observăm că oricare traseu din poziția (1,1) în poziția (n,m), are respectă regulile de deplasare, va face exact n-1 pași spre dreapta și exact m-1 pași în jos. Traseele diferă numai prin ordinea acestor pași, nu prin numărul lor!
Atunci numărul de trasee este egal cu numărul de combinații de n-1 pași spre stânga și m-1 pași spre în jos; altfel spus n+m-2 pași, dintre care n-1 sunt în jos, adică: \(C_{n+m-2}^{n-1}\).
Observații
- numărul de trasee crește foarte repede. Pentru valori relativ mici ale lui
nșimse produce overflow. Pentru valori mai mari ale acestora este necesară implementarea operațiilor cu numere mari! - de multe ori, pentru a rezolva problema cu valori mai mari ale lui
nșim, fără însă a implementa operații cu numere mari, se cere determinarea restului împărțirii rezultatului la o valoare datăMOD, adică realizarea operațiilor moduloMOD! - rezolvarea cu programare dinamică are complexitatea timp \(O(n \cdot m)\). Spațiul de memorie poate fi optimizat, folosind doar două tablouri unidimensionale, unul pentru linia curentă și celălalt pentru linia precedentă. Asta deoarece în calculul valorilor de pe linia curentă
ise folosesc doar elemente de pe aceasta și de pe linia precedentă,i-1. - complexitatea rezolvării cu combinări este cea a algoritmului de determinare a combinărilor. Acestea pot fi determinate fie folosind formula uzuală, fie folosind triunghiul lui Pascal.
Probleme propuse
Secvența de sumă maximă
Introducere
Se dă un tablou A cu n elemente întregi. Să se determine o secvență pentru care suma elementelor este maximă.
Problema este una clasică și admite diverse soluții. Vom vedea în continuare trei soluții, de complexități diferite! Să observăm însă că, dacă elementele ar fi pozitive, atunci secvența cerută ar fi întreg tabloul.
În continuare vom numi secvență candidat o secvență care ar putea fi secvența cerută.
Soluția 1
Prima soluție are complexitatea \(O(n^3)\) și poate fi folosită când valoarea lui n este în jur de 100.
Fiecare secvență a vectorului poate fi secvență candidat. Vom identifica toate secvențele delimitate de indicii i j, cu 1 ≤ i ≤ j ≤ n. Pentru fiecare secvență, vom determina suma elementelor care o compun și vom reține secvența de sumă maximă:
int st = 0 , dr = 1 , Smax = -2000000000 , S;
for(int i = 1 ; i <= n ; ++ i)
for(int j=i;j<=n;++j)
{
S = 0;
for(int k = i ; k <= j ; ++ k)
S += A[k];
if(S > Smax)
Smax = S, st = i, dr = j;
}
cout << Smax << endl;
cout << st << " " << dr;
Soluția 2
Soluția anterioară poate fi îmbunătățită folosind sume partiale pentru a determina suma elementelor din secvența i j. În acest mod complexitatea scade la \(O(n^2)\) și poate fi folosită când valoarea lui n este în jur de 1000.
SP[0] = 0;
for(int i =1 ; i <= n ; i ++)
SP[i] = SP[i-1] + A[i];
int st = 0 , dr = 1 , Smax = -2000000000 , S;
for(int i = 1 ; i <= n ; ++ i)
for(int j=i;j<=n;++j)
{
S = SP[j] - SP[i-1];
if(S > Smax)
Smax = S, st = i, dr = j;
}
cout << Smax << endl;
cout << st << " " << dr;
Soluția 3
Ultima soluție, de complexitate liniară – \(O(n)\) pleacă de la ideea că dacă într-o secvență (PQ), formată prin reuniunea (lipirea) secvențelor (P) și (Q), suma elementelor din secvența (P) este negativă, atunci suma elementelor din sevența (Q) este mai mare decât suma elementelor din secvența (PQ). În cest caz secvența (PQ) nu mai este secvență candidat, dar (Q) este (probabil) secvență candidat.
Procedăm astfel:
- parcurgem tabloul și adunăm elementul curent
A[i]laS– acesta reprezentând suma elementelor dintr-o secvență candidat; - dacă
Seste mai mare decât suma maximă, actualizăm rezultatele; - dacă
Sdevine negativ, îl reinițializăm la0; tot acum reinițializăm și poziția de început a secvenței candidat.
int st , dr, Smax = -2000000000 , S = -1, start;
for(int i = 1 ; i <= n ; ++ i)
{
if(S < 0)
S = 0, start = i;
S += A[i];
if(S > Smax)
Smax = S, st = start, dr = i;
}
cout << Smax << endl;
cout << st << " " << dr;
Soluția de mai sus poate fi utilizată pentru valori mai mari ale lui n, de exemplu 100000 sau 1000000. De asemenea, poate fi ușor modificată încât să se evite folosirea tabloului, determinând rezultatul direct din citire. Astfel, complexitatea spațiu a algoritmului devine \(O(1)\).
Probleme propuse
Liste liniare simplu înlănțuite alocate dinamic
O listă liniară simplu înlănțuită conține elemente (noduri) a căror valori constau din două părți: informația utilă și informația de legătură. Informația utilă reprezintă informația propriu-zisă memorată în elementul liste (numere, șiruri de caractere, etc.), iar informația de legătură precizează adresa următorului element al listei. În C/C++ putem folosi următorul tip de date pentru a memora elementele unei liste liniare simplu înlănțuite alocate dinamic:
struct nod{
int info;
nod * urm;
};
Câmpul info al tipului nod reprezintă informația utilă – în acest caz un număr întreg, iar câmpul urm este de tip pointer la nod și reprezintă informația de legătură.
În program vom folosi o variabilă de tip pointer (de exemplu prim) pentru a memora adresa primului element al listei și fiecare element al listei, începând cu primul, va memora în câmpul urm adresa elementului următor. Excepție face ultimul element al listei care va memora în câmpul urm valoarea NULL.
Observații:
- La început
primva avea valoareaNULL, cu semnificația că lista este vidă. Dacă la un moment dat lista redevine vidă (de exemplu se șterg toate elementele ei) variabilaprimva avea valoareaNULL. - Elementele listei sunt variabile dinamice, create cu ajutorul operatorului C++
newși gestionate prin intermediul pointerilor. Variabilaprimeste de tip pointer, dar este (în cele ce urmează) statică. - Fiind variabile dinamice, pentru elementele listei se alocă memorie în HEAP.
- Informațiile de legătură ocupă memorie. Spațiul de memorie ocupat de un pointer depinde de versiunea compilatorului folosit; în general este de
4octeți. Astfel, fiecare element al unei liste de tipul de mai sus va ocupa în memorie4+4=8octeți. - Accesul la un nod al listei se face prin parcurgerea nodurilor care îl preced.
O secvență C++ care conține declarațiile corespunzătoare poate fi:
struct nod{
int info;
nod * urm;
};
nod * prim = NULL;
În continuare vom prezenta secvențe/funcții C++ pentru principalele operații:
- crearea unui element nou,
- adăugarea unui element la sfârșitul listei,
- adăugarea unui element la începutul listei,
- parcurgerea listei,
- ștergere unui element din listă,
- inserarea unui element în listă.
Funcțiile care urmează vor avea ca parametru adresa primului element al listei și eventual alți parametri. În funcție de situație, parametrul care reprezintă adresa primului element ale listei va fi transmis prin valoare sau prin referință.
Crearea unui element nou
Numeroase operații cu liste solicită crearea unui nou element/nod. Pentru aceasta trebuie să ținem cont de următoarele:
- Nodurile sunt variabile dinamice. Crearea unui nou nod înseamnă crearea unei variabile dinamice. Acest lucru se face cu ajutorul operatorului C++
new, care are ca rezultat adresa variabilei nou create. Aceasta va fi memorată într-un pointer de tipnod *. Să-l numimp:nod * p = new nod; - Nodurile sunt variabile de tip structură, cu câmpurile
infoșiurm. Accesul la câmpuri se va face prin intermediul pointerilor, cu ajutorul operatorului->, astfel:p->infoșip->urm. Accesul la câmpuri se poate face și după dereferențierea pointer-ului:(* p).infoși(* p).urm. - Nodul nou creat va fi inclus într-o listă.
p->urmva memora adresa următorului element, sauNULLdacă nu există următorul element! - Rezumat:
peste pointer lanod; este de tipnod *;*peste variabila de tipnod– este nod din listăp->infoeste informația utilă din nodul listei, de tipintp->urmeste pointer. Memorează adresa elementului următor!
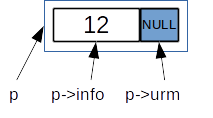
Secvența C++:
nod * p = new nod; p->info = ..... ; // cin >> p->info; p->urm = NULL;
Ne imaginăm lista în felul următor; săgețile simbolizează legăturile dintre nodurile listei. Vârful săgeții reprezintă elementul următor. Ultimul element nu are săgeată. Valoarea corespunzătoare din câmpul urm este NULL.
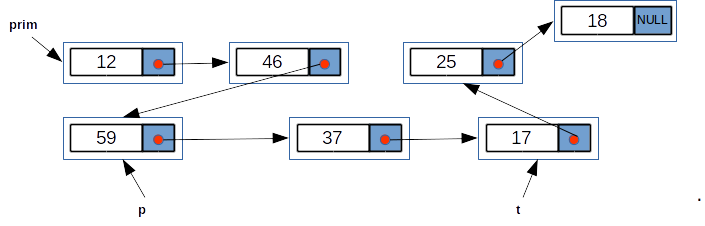
În exemplul de mai sus au loc următoarele relații:
- valoarea pointerului
primeste adresa elementului cu valoarea12; prim->info==12prim->urm->info==46prim->urmeste adresa elemenului cu valoarea46prim->urm->urm==pp->info==59p->urm->urm==tt->info==17t->urm->info==25t->urm->urm->info==18t->urm->urm->urm==NULLt->urm->urm->urm->infonu există. Rezultatul acestei expresii este impredictibil!
Adăugarea unui element la finalul listei
Un antet posibil pentru funcția care adaugă un element la finalul liste ar putea fi:
void AdaugaFinal(nod * & prim , int val);
Parametru prim este transmis prin referință pentru a trata corespunzător situația când lista este vidă. În acesta caz, valoare de intrare a lui prim este NULL, iar valoarea de ieșire este adresa primului element al listei – element nou creat.
Practic, vom trata două situații:
- dacă
primesteNULL, creăm un nod nou, care va fi primul și totodată ultimul element al listei, memorăm în el valoarea dorită șiprimdevine adresa acestui nod; - în caz contrar, identificăm ultimul nod al listei și nodul nou creat devine succesor al ultimului element și totodată ultimul element al listei.
void AdaugaFinal(nod * & prim , int x)
{
// creăm nod nou
nod * q = new nod;
q -> info = x;
q -> urm = NULL;
// adăugă noul nod la listă
if(prim == NULL)
{ // lista este vidă
prim = q;
}
else
{ // lista nu este vidă
nod * t = prim;
while(t -> urm != NULL)
t = t -> urm;
t -> urm = q;
}
}
Adăugarea unui element la începutul listei
Un antet posibil pentru funcția care adaugă element la începutul liste ar putea fi:
void AdaugaInceput(nod * & prim , int val);
Parametru prim este transmis prin referință deoarece la fiecare apel al funcției primul element se modifică; se creează un element nou care devine prim element al listei. Astfel, adresa primului element se modifică.
Procedăm astfel:
primmemorează adresa primului element- creăm un element nou:
nod * t = new nod; - memorăm în el informația utilă:
t->info = .... - îl plasăm în listă înaintea primului element:
t->urm = prim; - elementul nou creat este reținut ca prim element al listei:
prim = t;
Obs: Nu este necesară tratarea diferențiată a situațiilor când lista este vidă (prim==NULL), respectiv când lista conține elemente (prim memorează adresa primului element). În ambele situații atribuirea prim = t; are efectul dorit!
void AdaugaInceput(nod * & prim , int x)
{
// creăm nod nou
nod * t = new nod;
t -> info = x;
// legam nodul de lista
t -> urm = prim;
// valoarea lui prim se modifică, pentru a ieși din funcție cu valoarea corectă
prim = t;
}
Parcurgerea listei
Parcurgerea listei reprezintă vizitarea succesivă a elementelor pentru a realiza diverse operații cu valorile lor. Un antet posibil pentru o funcție care parcurge lista poate fi:
void Parcurgere(nod * prim);
Parcurgerea se realizează secvențial, element cu element:
- folosim un pointer
nod * pîn care vom memora, pe rând, adresele elementelor din listă; - începem de la primul element al listei:
p = prim; - cât timp nu am trecut de ultimul element:
- prelucrăm elementul curent (
p->info) - trecem la următorul element:
p = p->urm;
- prelucrăm elementul curent (
void Parcurgere(nod * prim)
{
nod * p = prim;
while(p != NULL)
{
//prelucrăm nodul curent
// trecem la următorul nod
p = p->urm;
}
}
Ștergerea unui element
Ștergerea unui element al listei constă în două etape: ștergerea propriu-zisă a variabilei dinamice în care este stoca nodul de șters și refacerea legăturilor, astfel încât lista să fie consistentă. Tehnic, modul de ștergere diferă după cum nodul de șters este primul din listă sau nu.
Dacă ștergem primul element al listei vom proceda astfel:
- memorăm adresa primului nod într-un pointer auxiliar:
nod * t = prim; - nodul de după
primdevine primul nod al listei:prim = prim->urm; - ștergem variabila adresată de
t:delete t;
Dac ștergem un element oarecare al listei, trebuie să cunoaștem într-un pointer oarecare, să spunem p, adresa elementului din fața nodului de șters. Acest lucru este necesar pentru refacerea corectă a legăturilor dintre elementele listei:
- vom șterge elementul situat în listă după cel cu adresa memorată în
p, adică vom ștergep->urm; - memorăm adresa nodului de șters înt-un pointer auxiliar:
nod * t = p->urm; - corectăm adresa elementului de după
p:p->urm = t->urm; - ștergem variabila adresată de
t:delete t;
Inserarea unui nou element
Și inserarea se face diferit, în funcție de poziția noului nod în listă; inserarea unui nod nou înaintea primului nod al listei (adresa sa este memorată în pointer-ul prim) se face astfel:
- creăm un nod nou:
nod * t = new nod; - memorăm valoarea dorită în acest nod:
t->info = ...; - îl legăm de primul nod al listei:
t->urm = prim; - nodul nou creat devine primul din listă:
prim = t;
Dacă nodul nou creat nu va fi primul din listă, îl vom insera după un nod cu adresa cunoscută, memorată în pointer-ul p:
- creăm un nod nou:
nod * t = new nod; - memorăm valoarea dorită în acest nod:
t->info = ...; - în inserăm în listă:
- nodul nou creat va fi înaintea nodului de după
p:t->urm = p->urm; - nodul nou creat va fi plasat după nodul
p:p->urm = t;
- nodul nou creat va fi înaintea nodului de după
Matrice Fibonacci
Introducere
Șirul lui Fibonacci este definit astfel:
$$ F_n = \begin{cases}
1& \text{dacă } n = 1 \text{ sau } n = 2 ,\\
F_{n-1} + F_{n-2} & \text{dacă } n > 2.
\end{cases} $$
Pentru a determina al n-termen a șirului putem folosi diverse metode. Acest articol prezintă un algoritm de complexitate \(O(n)\) care determină al n-lea termen.
Prezentul articol prezintă un algoritm de complexitate logaritmică, bazat pe înmulțirea rapidă a matricelor.
Matrice Fibonacci
Considerăm următoarea matrice: \( Q = \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right) \). Dacă extindem șirul lui Fibonacii cu încă un element, \( F_0 = 0 \), observăm că: \( Q = \left( \begin{matrix} F_2& F_1\\ F_1& F_0\end{matrix} \right) \). Să calculăm \(Q^2\) și \(Q^3\):
$$ \begin{align} Q^2 & = Q \times Q \\
& = \left( \begin{matrix} F_2& F_1\\ F_1& F_0\end{matrix} \right) \times \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right)\\
& = \left( \begin{matrix}
F_2 \cdot 1 + F_1 \cdot 1& F_2 \cdot 1 + F_1 \cdot 0 \\
F_1 \cdot 1 + F_0 \cdot 1& F_1 \cdot 1 + F_0 \cdot 0
\end{matrix} \right) \\
& = \left( \begin{matrix}
F_2 + F_1 & F_2 \\
F_1 + F_0 & F_1
\end{matrix} \right) \\
& = \left( \begin{matrix}
F_3 & F_2 \\
F_2 & F_1
\end{matrix} \right) \\
\end{align}
$$
Similar:
$$ \begin{align} Q^3 & = Q^2 \times Q \\
& = \left( \begin{matrix} F_3 & F_2\\ F_2 & F_1\end{matrix} \right) \times \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right)\\
& = \left( \begin{matrix}
F_3 \cdot 1 + F_2 \cdot 1& F_3 \cdot 1 + F_2 \cdot 0 \\
F_2 \cdot 1 + F_1 \cdot 1& F_2 \cdot 1 + F_1 \cdot 0
\end{matrix} \right) \\
& = \left( \begin{matrix}
F_3 + F_2 & F_3 \\
F_2 + F_1 & F_2
\end{matrix} \right) \\
& = \left( \begin{matrix}
F_4 & F_3 \\
F_3 & F_2
\end{matrix} \right) \\
\end{align}
$$
Observăm că \( Q^n = \left( \begin{matrix} F_{n+1}& F_n\\ F_n& F_{n-1}\end{matrix} \right) \), lucru ușor de demonstrat prin inducție matematică.
Concluzie: Dacă \( Q = \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right) \), atunci \( Q^n = \left( \begin{matrix} F_{n+1}& F_n\\ F_n& F_{n-1}\end{matrix} \right) \).
Algoritm
Pentru a determina \(F_n\), considerăm matricea \( Q = \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right) \), pe care o ridicăm la puterea n. Pentru a efectua repede calculele, folosim exponențierea rapidă.
Problema #Fibonacci2 cere determinarea celui de-al n-lea termen al șirului lui Fibonacii, modulo 666013. Succes!