Detalii evaluare #17788010
Rezumat problemă
#2124
Ornament
Gigel vrea să confecţioneze un ornament pentru pomul de iarnă format din pătrăţele frumos colorate. Pătrăţelele pot arăta ca în desenul alăturat. Se observă faptul că ele pot avea 4 culori diferite pe cele 4 laturi, 3, 2 sau chiar o singură culoare pe toate cele 4 laturi ale pătrăţelului.
Gigel are la dispoziţie n (n pătrat perfect) pătrăţele egale de acest tip cu laturile colorate doar în patru culori (alb, roşu, galben, albastru). Le vom numerota simplu de la 1 la 4.
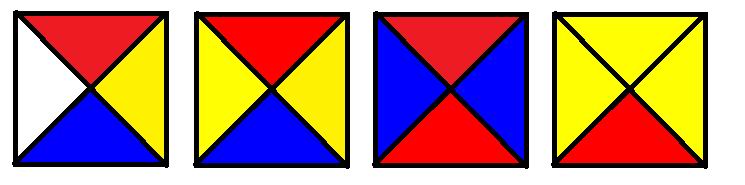
Să se scrie un program care primeşte o listă de n pătrăţele colorate şi determină o aranjare a lor sub forma de pătrat de forma k•k (k•k = n) astfel încât două laturi adiacente să aibă aceeaşi culoare, precum şi numărul de astfel de aranjări.
Olimpiada Municipala Informatica Iasi 2015
- Fișiere
-
Peticaru Alexandru (AlexandruPeticaru)
- Marinel Serban
- concurs
Detalii
| Problema | Ornament | Operații I/O |
ornament.in/ornament.out
|
|---|---|---|---|
| Limita timp | 0.2 secunde | Limita memorie |
Total: 2 MB
/
Stivă 1 MB
|
| Id soluție | #17788010 | Utilizator |
Bogdan Rizescu (rizescubogdan01)
|
| Fișier | ornament.cpp | Dimensiune | 1.25 KB |
| Data încărcării | 20 Octombrie 2019, 18:58 | Scor / rezultat | 100 puncte |
Evaluare
Mesaj compilare
Rezultat evaluare
| Test | Timp | Mesaj evaluare | Scor posibil | Scor obținut | ||
|---|---|---|---|---|---|---|
| 1 | 0 secunde | OK | 5 | 5 | Exemplu | |
| 2 | 0 secunde | OK | 5 | 5 | ||
| 3 | 0 secunde | OK | 5 | 5 | ||
| 4 | 0 secunde | OK | 5 | 5 | ||
| 5 | 0 secunde | OK | 5 | 5 | ||
| 6 | 0 secunde | OK | 5 | 5 | ||
| 7 | 0 secunde | OK | 5 | 5 | ||
| 8 | 0 secunde | OK | 5 | 5 | ||
| 9 | 0 secunde | OK | 5 | 5 | ||
| 10 | 0 secunde | OK | 5 | 5 | ||
| 11 | 0 secunde | OK | 5 | 5 | ||
| 12 | 0 secunde | OK | 5 | 5 | ||
| 13 | 0 secunde | OK | 5 | 5 | ||
| 14 | 0.032 secunde | OK | 5 | 5 | ||
| 15 | 0 secunde | OK | 5 | 5 | ||
| 16 | 0 secunde | OK | 5 | 5 | ||
| 17 | 0 secunde | OK | 5 | 5 | ||
| 18 | 0 secunde | OK | 5 | 5 | ||
| 19 | 0 secunde | OK | 5 | 5 | ||
| 20 | 0.08 secunde | OK | 5 | 5 | ||
| Punctaj total | 100 | |||||
Cum funcționează evaluarea?
www.pbinfo.ro permite evaluarea a două tipuri de probleme:
- probleme la care rezolvarea presupune scrierea unui program complet
- probleme la care rezolvarea presupune scrierea unei secvențe de program - câteva instrucțiuni, o listă de declarații, una sau mai multe funcții, etc.
Problema Ornament face parte din prima categorie. Soluția propusă de tine va fi evaluată astfel:
- Programul sursă este compilat folosind compilatorul corespunzător. Dacă în urma compilării se obțin erori sau avertismente, acestea sunt afișate în această pagină.
- Dacă programul a fost compilat, executabilul obținut va fi rulat, furnizându-i-se unul sau mai multe seturi de date de intrare, în concordanță cu restricțiile specifice problemei. Pentru fiecare set de date se obține un anumit punctaj, în raport cu corectitudinea soluției tale.
Suma punctajelor acordate pe testele utilizate pentru verificare este 100. Astfel, soluția ta poate obține cel mult 100 de puncte, caz în care se poate considera corectă.