Articolele lui Candale Silviu (silviu)

Introducere

Se dă un tablou A cu n elemente întregi. Să se determine o secvență pentru care suma elementelor este maximă.

Problema este una clasică și admite diverse soluții. Vom vedea în continuare trei soluții, de complexități diferite! Să observăm însă că, dacă elementele ar fi pozitive, atunci secvența cerută ar fi întreg tabloul.

În continuare vom numi secvență candidat o secvență care ar putea fi secvența cerută.

Soluția 1

Prima soluție are complexitatea \(O(n^3)\) și poate fi folosită când valoarea lui n este în jur de 100.

Fiecare secvență a vectorului poate fi secvență candidat. Vom identifica toate secvențele delimitate de indicii i j, cu 1 ≤ i ≤ j ≤ n. Pentru fiecare secvență, vom determina suma elementelor care o compun și vom reține secvența de sumă maximă:

int st = 0 , dr = 1 , Smax = -2000000000 , S;
for(int i = 1 ; i <= n ; ++ i)
    for(int j=i;j<=n;++j)
    {
        S = 0;
        for(int k = i ; k <= j ; ++ k)
            S += A[k];
        if(S > Smax)
            Smax = S, st = i, dr = j;
    }
cout << Smax << endl;
cout << st << " " << dr;

Soluția 2

Soluția anterioară poate fi îmbunătățită folosind sume partiale pentru a determina suma elementelor din secvența i j. În acest mod complexitatea scade la \(O(n^2)\) și poate fi folosită când valoarea lui n este în jur de 1000.

SP[0] = 0;
for(int i =1 ; i <= n ; i ++)
    SP[i] = SP[i-1] + A[i];
int st = 0 , dr = 1 , Smax = -2000000000 , S;
for(int i = 1 ; i <= n ; ++ i)
    for(int j=i;j<=n;++j)
    {
        S = SP[j] - SP[i-1];
        if(S > Smax)
            Smax = S, st = i, dr = j;
    }
cout << Smax << endl;
cout << st << " " << dr;

Soluția 3

Ultima soluție, de complexitate liniară – \(O(n)\) pleacă de la ideea că dacă într-o secvență (PQ), formată prin reuniunea (lipirea) secvențelor (P) și (Q), suma elementelor din secvența (P) este negativă, atunci suma elementelor din sevența (Q) este mai mare decât suma elementelor din secvența (PQ). În cest caz secvența (PQ) nu mai este secvență candidat, dar (Q) este (probabil) secvență candidat.

Procedăm astfel:

• parcurgem tabloul și adunăm elementul curent A[i] la S – acesta reprezentând suma elementelor dintr-o secvență candidat;
• dacă S este mai mare decât suma maximă, actualizăm rezultatele;
• dacă S devine negativ, îl reinițializăm la 0; tot acum reinițializăm și poziția de început a secvenței candidat.

int st , dr, Smax = -2000000000 , S = -1, start;
for(int i = 1 ; i <= n ; ++ i)
{
    if(S < 0)
        S = 0, start = i;
    S += A[i];
    if(S > Smax)
        Smax = S, st = start, dr = i;
}
cout << Smax << endl;
cout << st << " " << dr;

Soluția de mai sus poate fi utilizată pentru valori mai mari ale lui n, de exemplu 100000 sau 1000000. De asemenea, poate fi ușor modificată încât să se evite folosirea tabloului, determinând rezultatul direct din citire. Astfel, complexitatea spațiu a algoritmului devine \(O(1)\).

Probleme propuse

• #SecvSumMax
• #ursulet

Introducere

Problema #divimax cere, printre altele, determinarea celui mai mare număr care poate fi obținut prin concatenarea unor numere cunoscute.

De exemplu, pentru 15 234 1024, rexultatul va fi 234151024. La prima vedere, trebuie să sortăm numerele în ordine lexicografică inversă. Într-adevăr, ordonând numerele lexicografic invers, obținem 234 15 1024, iar prin concatenare obținem rezultatul de mai sus.

Dacă însă numere sunt 441 24 4, ordinea lexicografică (inversă) este 441 4 24. Prin concatenare obținem 441424, dar luându-le în ordinea 4 441 24 obținem un număr mai mare, 444124. Problema apare și atunci când dorim să obținem cel mai mic număr care poate fi obținut prin concatenarea unor numere date – simpla ordonare lexicografică nu este suficientă.

Problema

Considerăm următoarea cerință: Se dau două numere naturale A și B. Să se stabilească ordinea celor două valori, atfel încât numărul obținut prin concatenare să fie mai mic. Pentru 1024 și 15, răspunsul este 1024 15, iar pentru 331 3, răspunsul este 331 3.

Algoritm

Procedăm astfel:

• considerăm numărul x, obținut prin concatenarea lui A cu B;
• considerăm numărul y, obținut prin concatenarea lui B cu A;
• dacă x < y, atunci ordinea dorită este A B;
• în caz contrar, ordinea este B A.

Secvențe C++

Următoarele funcții C++ verifică dacă pentru a obține prin concatenarea numerelor A și B un număr mai mic le păstrăm sau nu ordinea. Returnează true dacă ordinea este A B, respectiv false dacă ordinea este B A. Ele pot fi folosite pentru a sorta un tablou folosind funcția STL sort().

Prima variantă construiește cele două numere descrise mai sus și le compară. Valorile lui A și B trebuie să fie suficient de mici încât să le putem concatena fără overflow!

bool Compare(int A , int B){
    int pA = 1, pB = 1, x = A, y = B;
    do pA *= 10, x /= 10; while(x);
    do pB *= 10, y /= 10; while(y);
    return 1LL * A * pB + B < 1LL * B * pA + A;
}

Următoarea secvență folosește funcția std::to_string(), construiește două stringuri și le verifică ordinea (lexicografică). Din păcate este lentă!

bool Compare(int A , int B){
    return to_string(A) + to_string(B) < to_string(B) + to_string(A);
}

Următoarea secvență construiește două tablouri cu cifrele celor două numere obținute prin concatenare și compară lexicografic tablourile.

bool Compare(int A , int B){
    int v[30], u[30];
    v[0] = u[0] = 0;
    while(A)
        v[++v[0]] = A % 10, A /= 10;
    while(B)
        u[++u[0]] = B % 10, B /= 10;
    std::reverse(v + 1, v + v[0] + 1);
    std::reverse(u + 1, u + u[0] + 1);
    int lgv = v[0] , lgu = u[0];
    for(int i = 1 ; i <= lgu; i ++)
        v[++v[0]] = u[i];
    for(int i = 1 ; i <= lgv; i ++)
        u[++u[0]] = v[i];
    //aici v[0] == u[0]
    for(int i = 1 ; i <= v[0] ; i ++)
         if(v[i] < u[i])
              return true;
         else
            if(v[i] > u[i])
                 return false;
    return false;
}

Observații:

• în secvența de mai sus, dimensiunile tablourilor v și u se memorează în V[0], resectiv u[0];
• reverse este o funcție STL, disponibilă în headerul algorithm, care oglindește tabloul
• utilizăm faptul că, prin construcția lor, cele două tablouri au aceeași lungime. În caz contar, algoritmul este incomplet!

O listă liniară simplu înlănțuită conține elemente (noduri) a căror valori constau din două părți: informația utilă și informația de legătură. Informația utilă reprezintă informația propriu-zisă memorată în elementul liste (numere, șiruri de caractere, etc.), iar informația de legătură precizează adresa următorului element al listei. În C/C++ putem folosi următorul tip de date pentru a memora elementele unei liste liniare simplu înlănțuite alocate dinamic:

struct nod{
  int info;
  nod * urm;
};

Câmpul info al tipului nod reprezintă informația utilă – în acest caz un număr întreg, iar câmpul urm este de tip pointer la nod și reprezintă informația de legătură.

În program vom folosi o variabilă de tip pointer (de exemplu prim) pentru a memora adresa primului element al listei și fiecare element al listei, începând cu primul, va memora în câmpul urm adresa elementului următor. Excepție face ultimul element al listei care va memora în câmpul urm valoarea NULL.

Observații:

• La început prim va avea valoarea NULL, cu semnificația că lista este vidă. Dacă la un moment dat lista redevine vidă (de exemplu se șterg toate elementele ei) variabila prim va avea valoarea NULL.
• Elementele listei sunt variabile dinamice, create cu ajutorul operatorului C++ new și gestionate prin intermediul pointerilor. Variabila prim este de tip pointer, dar este (în cele ce urmează) statică.
• Fiind variabile dinamice, pentru elementele listei se alocă memorie în HEAP.
• Informațiile de legătură ocupă memorie. Spațiul de memorie ocupat de un pointer depinde de versiunea compilatorului folosit; în general este de 4 octeți. Astfel, fiecare element al unei liste de tipul de mai sus va ocupa în memorie 4+4=8 octeți.
• Accesul la un nod al listei se face prin parcurgerea nodurilor care îl preced.

O secvență C++ care conține declarațiile corespunzătoare poate fi:

struct nod{
  int info;
  nod * urm;
};

nod * prim = NULL;

În continuare vom prezenta secvențe/funcții C++ pentru principalele operații:

• crearea unui element nou,
• adăugarea unui element la sfârșitul listei,
• adăugarea unui element la începutul listei,
• parcurgerea listei,
• ștergere unui element din listă,
• inserarea unui element în listă.

Funcțiile care urmează vor avea ca parametru adresa primului element al listei și eventual alți parametri. În funcție de situație, parametrul care reprezintă adresa primului element ale listei va fi transmis prin valoare sau prin referință.

Crearea unui element nou

Numeroase operații cu liste solicită crearea unui nou element/nod. Pentru aceasta trebuie să ținem cont de următoarele:

• Nodurile sunt variabile dinamice. Crearea unui nou nod înseamnă crearea unei variabile dinamice. Acest lucru se face cu ajutorul operatorului C++ new, care are ca rezultat adresa variabilei nou create. Aceasta va fi memorată într-un pointer de tip nod *. Să-l numim p: nod * p = new nod;
• Nodurile sunt variabile de tip structură, cu câmpurile info și urm. Accesul la câmpuri se va face prin intermediul pointerilor, cu ajutorul operatorului ->, astfel: p->info și p->urm. Accesul la câmpuri se poate face și după dereferențierea pointer-ului: (* p).info și (* p).urm.
• Nodul nou creat va fi inclus într-o listă. p->urm va memora adresa următorului element, sau NULL dacă nu există următorul element!
• Rezumat:
  • p este pointer la nod; este de tip nod *;
  • *p este variabila de tip nod – este nod din listă
  • p->info este informația utilă din nodul listei, de tip int
  • p->urm este pointer. Memorează adresa elementului următor!

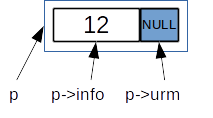
Secvența C++:

nod * p = new nod;
p->info = ..... ; // cin >> p->info;
p->urm = NULL;

Ne imaginăm lista în felul următor; săgețile simbolizează legăturile dintre nodurile listei. Vârful săgeții reprezintă elementul următor. Ultimul element nu are săgeată. Valoarea corespunzătoare din câmpul urm este NULL.

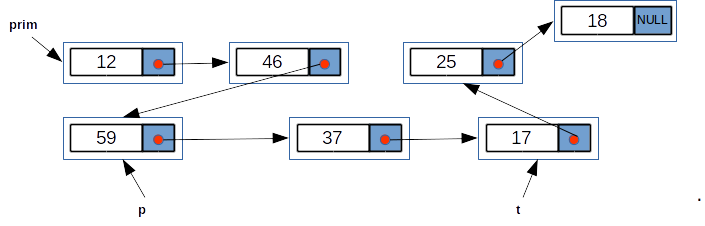
În exemplul de mai sus au loc următoarele relații:

• valoarea pointerului prim este adresa elementului cu valoarea 12;
• prim->info==12
• prim->urm->info==46
• prim->urm este adresa elemenului cu valoarea 46
• prim->urm->urm==p
• p->info==59
• p->urm->urm==t
• t->info==17
• t->urm->info==25
• t->urm->urm->info==18
• t->urm->urm->urm==NULL
• t->urm->urm->urm->info nu există. Rezultatul acestei expresii este impredictibil!

Adăugarea unui element la finalul listei

Un antet posibil pentru funcția care adaugă un element la finalul liste ar putea fi:

void AdaugaFinal(nod * & prim , int val);

Parametru prim este transmis prin referință pentru a trata corespunzător situația când lista este vidă. În acesta caz, valoare de intrare a lui prim este NULL, iar valoarea de ieșire este adresa primului element al listei – element nou creat.

Practic, vom trata două situații:

• dacă prim este NULL, creăm un nod nou, care va fi primul și totodată ultimul element al listei, memorăm în el valoarea dorită și prim devine adresa acestui nod;
• în caz contrar, identificăm ultimul nod al listei și nodul nou creat devine succesor al ultimului element și totodată ultimul element al listei.

void AdaugaFinal(nod * & prim , int x)
{
  // creăm nod nou
  nod * q = new nod;
  q -> info = x;
  q -> urm = NULL;
  // adăugă noul nod la listă
  if(prim == NULL)
  { // lista este vidă
    prim = q;
  }
  else
  { // lista nu este vidă
    nod * t = prim;
    while(t -> urm != NULL)
      t = t -> urm;
    t -> urm = q;
  }
}

Adăugarea unui element la începutul listei

Un antet posibil pentru funcția care adaugă element la începutul liste ar putea fi:

void AdaugaInceput(nod * & prim , int val);

Parametru prim este transmis prin referință deoarece la fiecare apel al funcției primul element se modifică; se creează un element nou care devine prim element al listei. Astfel, adresa primului element se modifică.

Procedăm astfel:

• prim memorează adresa primului element
• creăm un element nou: nod * t = new nod;
• memorăm în el informația utilă: t->info = ....
• îl plasăm în listă înaintea primului element: t->urm = prim;
• elementul nou creat este reținut ca prim element al listei: prim = t;

Obs: Nu este necesară tratarea diferențiată a situațiilor când lista este vidă (prim==NULL), respectiv când lista conține elemente (prim memorează adresa primului element). În ambele situații atribuirea prim = t; are efectul dorit!

void AdaugaInceput(nod * & prim , int x)
{
  // creăm nod nou
  nod * t = new nod;
  t -> info = x;

  // legam nodul de lista
  t -> urm = prim;

  // valoarea lui prim se modifică, pentru a ieși din funcție cu valoarea corectă
  prim = t;
}

Parcurgerea listei

Parcurgerea listei reprezintă vizitarea succesivă a elementelor pentru a realiza diverse operații cu valorile lor. Un antet posibil pentru o funcție care parcurge lista poate fi:

void Parcurgere(nod * prim);

Parcurgerea se realizează secvențial, element cu element:

• folosim un pointer nod * p în care vom memora, pe rând, adresele elementelor din listă;
• începem de la primul element al listei: p = prim;
• cât timp nu am trecut de ultimul element:
  • prelucrăm elementul curent (p->info)
  • trecem la următorul element: p = p->urm;

void Parcurgere(nod *  prim)
{
  nod * p = prim;
  while(p != NULL)
  {
    //prelucrăm nodul curent

    // trecem la următorul nod
    p = p->urm;
  }
}

Ștergerea unui element

Ștergerea unui element al listei constă în două etape: ștergerea propriu-zisă a variabilei dinamice în care este stoca nodul de șters și refacerea legăturilor, astfel încât lista să fie consistentă. Tehnic, modul de ștergere diferă după cum nodul de șters este primul din listă sau nu.

Dacă ștergem primul element al listei vom proceda astfel:

• memorăm adresa primului nod într-un pointer auxiliar: nod * t = prim;
• nodul de după prim devine primul nod al listei: prim = prim->urm;
• ștergem variabila adresată de t: delete t;

Dac ștergem un element oarecare al listei, trebuie să cunoaștem într-un pointer oarecare, să spunem p, adresa elementului din fața nodului de șters. Acest lucru este necesar pentru refacerea corectă a legăturilor dintre elementele listei:

• vom șterge elementul situat în listă după cel cu adresa memorată în p, adică vom șterge p->urm;
• memorăm adresa nodului de șters înt-un pointer auxiliar: nod * t = p->urm;
• corectăm adresa elementului de după p: p->urm = t->urm;
• ștergem variabila adresată de t: delete t;

Inserarea unui nou element

Și inserarea se face diferit, în funcție de poziția noului nod în listă; inserarea unui nod nou înaintea primului nod al listei (adresa sa este memorată în pointer-ul prim) se face astfel:

• creăm un nod nou: nod * t = new nod;
• memorăm valoarea dorită în acest nod: t->info = ...;
• îl legăm de primul nod al listei: t->urm = prim;
• nodul nou creat devine primul din listă: prim = t;

Dacă nodul nou creat nu va fi primul din listă, îl vom insera după un nod cu adresa cunoscută, memorată în pointer-ul p:

• creăm un nod nou: nod * t = new nod;
• memorăm valoarea dorită în acest nod: t->info = ...;
• în inserăm în listă:
  • nodul nou creat va fi înaintea nodului de după p: t->urm = p->urm;
  • nodul nou creat va fi plasat după nodul p: p->urm = t;

Introducere

Se dă un șir cu n elemente. Să se determine cea mai lungă secvență de elemente din șir cu proprietatea că extremitățile secvenței au valori egale.

Fie V[] vectorul dat, cu n elemente. Vom propune trei soluții, cu diverse complexități.

Soluția 1

Prima soluție are complexitate \( O(n^2) \) și poate fi folosită pentru a rezolva problema #SecvEgale1 .

Considerăm că:

• n ≤ 1000
• elementele șirului au valori mai mici decât 231

Pentru fiecare element V[i] al vectorului vom determina cel mai mare indice j astfel încât V[i] și V[j] sunt egale. Dintre toate aceste perechi i j o reținem pe aceea pentru care lungimea secvenței, j - i + 1 este mai mare.

Soluția 2

Dacă valorile din șir sunt cuprinse între 1 și vmax, avem o soluție de complexitate \(O(n \cdot vmax)\). Pe site: #Lungime .

Considerăm că:

• n ≤ 100000
• elementele șirului au valori mai mici sau egale cu vmax=100.

Pentru fiecare valoare c de la 1 la vmax vom determina cel mai din stânga indice i și cel mai din dreapta indice j cu proprietatea că V[i] și V[j] sunt egale cu c. Reținem pereceha i j pentru care j - i + 1 este maxim.

Soluția 3

O soluție de complexitate \(O(n)\) poate fi implementată dacă vmax este suficient de mic pentru a construi un vector cu vmax elemente: #distanta_maxima , #Lungime1 , #SecvEgale1_v2 .

Considerăm că:

• n ≤ 100000
• elementele șirului au valori mai mici sau egale cu vmax=10000.

Considerăm un vector P[] în care P[k] reprezintă cel mai din stânga indice i cu proprietatea că V[i] = k. Inițial toate elementele lui P sunt nule.

Fie lgmax lungimera maximă a unei secvențe care respectă regula. Inițial, lgmax ← 0. Parcugem vectorul V:

• dacă P[V[i]] este zero, suntem la prima apariție a valorii curente V[i] în vector, deci cea mai din stânga. Atunci: P[V[i]] ← i.
• dacă P[V[i]] nu este zero, atunci valoarea V[i] a mai apărut în vector, la poziția P[V[i]]. Dacă i - P[V[i]] > lgmax, actualizăm lgmax și reținem secvența P[V[i]] i ca fiind secvența rezultat!

Introducere

Șirul lui Fibonacci este definit astfel:

$$ F_n = \begin{cases}
1& \text{dacă } n = 1 \text{ sau } n = 2 ,\\
F_{n-1} + F_{n-2} & \text{dacă } n > 2.
\end{cases} $$

Pentru a determina al n-termen a șirului putem folosi diverse metode. Acest articol prezintă un algoritm de complexitate \(O(n)\) care determină al n-lea termen.

Prezentul articol prezintă un algoritm de complexitate logaritmică, bazat pe înmulțirea rapidă a matricelor.

Matrice Fibonacci

Considerăm următoarea matrice: \( Q = \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right) \). Dacă extindem șirul lui Fibonacii cu încă un element, \( F_0 = 0 \), observăm că: \( Q = \left( \begin{matrix} F_2& F_1\\ F_1& F_0\end{matrix} \right) \). Să calculăm \(Q^2\) și \(Q^3\):

$$ \begin{align} Q^2 & = Q \times Q \\ & = \left( \begin{matrix} F_2& F_1\\ F_1& F_0\end{matrix} \right) \times \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right)\\ & = \left( \begin{matrix} F_2 \cdot 1 + F_1 \cdot 1& F_2 \cdot 1 + F_1 \cdot 0 \\ F_1 \cdot 1 + F_0 \cdot 1& F_1 \cdot 1 + F_0 \cdot 0 \end{matrix} \right) \\ & = \left( \begin{matrix} F_2 + F_1 & F_2 \\ F_1 + F_0 & F_1 \end{matrix} \right) \\ & = \left( \begin{matrix} F_3 & F_2 \\ F_2 & F_1 \end{matrix} \right) \\
\end{align}
$$

Similar:

$$ \begin{align} Q^3 & = Q^2 \times Q \\ & = \left( \begin{matrix} F_3 & F_2\\ F_2 & F_1\end{matrix} \right) \times \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right)\\ & = \left( \begin{matrix} F_3 \cdot 1 + F_2 \cdot 1& F_3 \cdot 1 + F_2 \cdot 0 \\ F_2 \cdot 1 + F_1 \cdot 1& F_2 \cdot 1 + F_1 \cdot 0 \end{matrix} \right) \\ & = \left( \begin{matrix} F_3 + F_2 & F_3 \\ F_2 + F_1 & F_2 \end{matrix} \right) \\ & = \left( \begin{matrix} F_4 & F_3 \\ F_3 & F_2 \end{matrix} \right) \\
\end{align}
$$

Observăm că \( Q^n = \left( \begin{matrix} F_{n+1}& F_n\\ F_n& F_{n-1}\end{matrix} \right) \), lucru ușor de demonstrat prin inducție matematică.

Concluzie: Dacă \( Q = \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right) \), atunci \( Q^n = \left( \begin{matrix} F_{n+1}& F_n\\ F_n& F_{n-1}\end{matrix} \right) \).

Algoritm

Pentru a determina \(F_n\), considerăm matricea \( Q = \left( \begin{matrix} 1& 1\\ 1& 0\end{matrix} \right) \), pe care o ridicăm la puterea n. Pentru a efectua repede calculele, folosim exponențierea rapidă.

Problema #Fibonacci2 cere determinarea celui de-al n-lea termen al șirului lui Fibonacii, modulo 666013. Succes!

Bibliografie

• http://mathworld.wolfram.com/FibonacciQ-Matrix.html

Considerăm un graf neorientat ponderat (cu costuri) conex G. Se numește arbore parțial un graf parțial al lui G care este arbore. Se numește arbore parțial de cost minim un arbore parțial pentru care suma costurilor muchiilor este minimă.

Dacă graful nu este conex, vorbim despre o pădure parțială de cost minim.

Algoritmul lui Kruskal permite determinarea unui arbore parțial de cost minim (APM) într-un graf ponderat cu N noduri.

Descrierea algoritmului

Pentru a determina APM-ul se pleacă de la o pădure formată din N subarbori. Fiecare nod al grafului reprezintă inițial un subarbore. Aceștia vor fi reuniți succesiv prin muchii, până când se obține un singur arbore (dacă graful este conex) sau până când acest lucru nu mai este posibil (dacă graful nu este conex).

Algoritmul este:

• se ordonează muchiile grafului crescător după cost;
• se analizează pe rând muchiile grafului, în ordinea crescătoare a costurilor;
• pentru fiecare muchie analizată:
  • dacă extremitățile muchiei fac parte din același subarbore, muchia se ignoră
  • dacă extremitățile muchiei fac parte din subarbori diferiți, aceștia se vor reuni, iar muchia respectivă face parte din APM.

Principala dificultate în algoritmul descris mai sus este stabilirea faptului că extremitățile muchiei curente fac sau nu parte din același subarbore. În acest scop vom stabili pentru fiecare subarbore un nod special, numit reprezentant al (sub)arborelui și pentru fiecare nod din graf vom memora reprezentantul său (de fapt al subarborelui din care face parte) într-un tablou unidimensional.

Pentru a stabili dacă două noduri fac sau nu parte din același subarbore vom verifica dacă ele au același reprezentant. Pentru a reuni doi subarbori vom înlocui pentru toate nodurile din subarborele B cu reprezentantul subarborelui A.

Înlocuirile descrise mai sus sunt simple dar lente. Pentru o implementare mai eficientă a algoritmului se poate folosi conceptul de Padure de mulțimi disjuncte, descris în acest articol.

Exemplu

Vom determina, folosind Algoritmul lui Kruskal, arborele parțial de cost minim pentru graful de mai jos:

Muchiile se vor analiza în ordinea următoare:

1.		Se adaugă muchia (7,8) de cost 1
2.		Se adaugă muchia (3,9) de cost 2
3.		Se adaugă muchia (6,7) de cost 2
4.		Se adaugă muchia (1,2) de cost 4
5.		Se adaugă muchia (3,6) de cost 1
6.		Se ignoră muchia (7,9) de cost 6
7.		Se adaugă muchia (3,4) de cost 7
8.		Se ignoră muchia (8,9) de cost 7
9.		Se adaugă muchia (1,8) de cost 8
10.		Se ignoră muchia (2,3) de cost 8
11.		Se adaugă muchia (4,5) de cost 9
12.		Se ignoră muchia (5,6) de cost 10
13.		Se ignoră muchia (2,8) de cost 11
14.		Se ignoră muchia (4,6) de cost 14

Secvență C++

Următoarea secvență determină costul total al APM-ului, folosind algoritmul lui Kruskal. Presupunem că graful are cel mult 100 de noduri.

struct muchie{
	int i,j,cost;
};

int n , m , t[101];

muchie x[5000];

int main()
{
    cin >> n >> m;

    for(int i = 0 ; i < m ; ++i)
		cin >> x[i].i >> x[i].j >> x[i].cost;

	//sortare tablou x[] după campul cost
    // ... de completat

    //initializare reprezentanti
	for(int i =1 ; i <= n ; ++i)
		t[i] = i;
      //determinare APM
	int S = 0;
	for(int i = 0 ; i < m ; i ++)
		if(t[x[i].i] != t[x[i].j]) // extremitatile fac parte din subrabori diferiti
		{
			S += x[i].cost;
            //reunim subarborii
			int ai = t[x[i].i], aj = t[x[i].j];
			for(int j =1 ; j <= n ; ++j)
				if(t[j] == aj)
					t[j] = ai;
		}
	cout << S << "\n";
	return 0;
}

Vezi și

• Algoritmul lui Prim

Operațiile standard de intrare/ieșire se fac cu tastatură și ecranul, dar este posibil să realizăm și citiri din fișiere text, respectiv scrieri în fișiere text. Pentru a realiza operațiile propriu-zise, fișierele sunt asociate cu fluxuri de date, iar operațiile sunt similare cu cele cu tastatura și ecranul.

Etapele lucrului cu fișiere text

În C++ există mai multe modalități de lucru cu fișiere text. Toate respectă următoarele etape:

1. deschiderea fișierului/asocierea fișierului cu un flux de date;
2. citirea din fișier/scrierea în fișier;
3. închiderea fișierului/fluxului de date

Deschiderea fișierului

O modalitate uzuală de a deschide fișiere constă în declararea unor variabile de tip flux. Acestea sunt de tip:

• ofstream pentru fluxurile de ieșire – asociate cu fișierele în care vom scrie;
• ifstream pentru fluxurile de intrare – asociate cu fișierele din care vom citi;

Declararea variabilelor se poate face astfel:

ifstream fin(NUME_FISIER_INTRARE);
ofstream fout(NUME_FISIER_IESIRE);

NUME_FISIER_INTRARE și NUME_FISIER_IESIRE sunt șiruri de caractere care conțin numele fișierelor din care se face citirea/în care se face scrierea, de exemplu:

ifstream fin("fisier.in");
ofstream fout("fisier.out");

Nu este obligatoriu să folosim extensiile .in și .out, dar ele sunt frecvent folosite în algoritmică, pentru a desemna fișierul de intrare (INput), respectiv fișierul de ieșire (OUTput.)

fin și fout sunt identificatori de variabile. Putem folosi orice identificator, dar alegerea unor nume clare precum fin și fout, sau is (input stream) și os (output stream) fac, considerăm noi, programele mai ușor de înțeles și depanat.

Secvența de mai sus realizează simultan două operații: declararea variabilei de tip flux și dechiderea acestuia (asocierea cu fișierul corespunzător). Ele pot fi realizate și independent, de exemplu astfel:

ifstream fin;
fin.open("fisier.in");

sau

fstream fin("fisier.in", ios::in), fout("fisier.out", ios::out);

Declararea variabilelor de tip flux se poate face oriunde, cu respectarea restricțiilor cunoscute: orice variabilă folosită trebuie să fi fost anterior declarată.

Citirea din fișier/scrierea în fișier

Pentru citirea propiu-zisă a datelor din fișier/scrierea datelor în fișier se folosesc operatorii de extracție din flux/inserare în flux.

De exemplu:

int x;
fin >> x;
fout << 2 * x;

Închiderea fișierelor

Se face astfel:

fin.close();
fout.close();

Un exemplu complet

Următorul program este soluție corectă pentru problema #sum :

#include <iostream>
#include <fstream>

using namespace std;

ifstream fin("sum.in");
ofstream fout("sum.out");

int main()
{
    int a , b, s;
    fin >> a >> b;
    fin.close();
    s = a + b;

    fout << s;
    fout.close();

    return 0;
}

Observații

• fișierele de intrare (deschise pentru citire) trebuie să existe. Dacă se deschide pentru citire un fișier care nu există, operațiile de citire (fin >> ...) vor eșua și comportamentul programului devine de multe ori impredictibil;
• fișierele de ieșire (deschise pentru scriere) nu trebuie să existe. La deschidere ele vor fi create. Dacă fișierul de ieșire există conținurul său va fi înlocuit cu datele scrise de programul care rulează.

Ridicarea la putere este o operație binecunoscută, formulă uzuală fiind: $$ A^n = \prod_{i=1}^n {A} = \underbrace{A \times A \times … \times A }_{\text{de } n \text{ ori}} $$

Un algoritm care implementează această metodă va avea complexitate liniară, \(O(n)\):

int Putere(int A , int n)
{
    int P = 1 ;
    for(int i = 1 ; i <= n ; i ++)
        P = P * A;
    return P;
}

Descriere

O metodă mai bună este cea numită exponențierea rapidă , sau ridicarea la putere în timp logaritmic, complexitatea sa fiind \(O(\log_2{n})\). Ea se bazează pe următoarea formulă:

$$ A^n = \begin{cases} 1& \text{, dacă } n = 0\\ A \cdot A^{n-1}& \text{, dacă } n \text{ – impar}\\ {\left(A^{\frac{n}{2}}\right)}^2& \text{, dacă } n \text{ – par} \end{cases}$$

Exemplu

Să calculăm \(2^{25}\):

• \(2^{25} = 2 \cdot 2^{24}\), deoarece 25 este impar
• \(2^{24} = {(2^{12})}^2\), deoarece 24 este par
• \(2^{12} = {(2^{6})}^2\), deoarece 12 este par
• \(2^{6} = {(2^{3})}^2\), deoarece 6 este par
• \(2^{3} = 2 \cdot 2^{2}\), deoarece 3 este impar
• \(2^{2} = {(2^{1})}^2\), deoarece 2 este par
• \(2^{1} = 2 \cdot 2^{0}\), deoarece 1 este impar
• \(2^{0} = 1\)

Atunci în ordine inversă:

• \(2^{1} = 2 \cdot 1 = 2\)
• \(2^{2} = {2}^2 = 4\)
• \(2^{3} = 2 \cdot 4 = 8\)
• \(2^{6} = {8}^2 = 64\)
• \(2^{12} = {64}^2 = 4096\)
• \(2^{24} = {4096}^2 = 16777216\)
• \(2^{25} = 2 \cdot 16777216 = 33554432\)

Constatăm că numărul înmulțirilor efectuate este mult mai mic decât în cazul primei metode.

Implementare recursivă

Implementarea recursivă este directă:

int Putere(int A , int n)
{
    if(n == 0)
        return 1;
    if(n % 2 == 1)
        return A * Putere(A , n - 1);
    int P = Putere(A , n / 2);
    return P * P;
}

Implementare iterativă

Să considerăm \(A^{25}\). Să-l scriem pe \(25\) ca sumă de puteri ale lui \(2\) (orice număr natural poate fi scris ca sumă de puteri ale lui \(2\) într-un singur mod): \(25 = 1 + 8 + 16\).

Atunci \( A^{25} = A^{1 + 8 + 16} = A^1 \cdot A^8 \cdot A^{16} = \underbrace{{(A^1)}^1}_{=A^1} \cdot \underbrace{{(A^2)}^0}_{=1} \cdot \underbrace{{(A^4)}^0}_{=1} \cdot \underbrace{{(A^8)}^1}_{=A^8} \cdot \underbrace{{(A^{16})}^1}_{=A^{16}}\). Observăm că exponenții \(0\) și \(1\) sunt cifrele reprezentării în baza \(2\) a lui \(25\).

Se figurează următoarea idee, pentru a determina An:

• vom determina un produs P, format din factori de forma A1, A2, A4, A8, …
• determinăm cifrele reprezentării în baza 2 a lui n, începând cu cea mai nesemnificativă:
  • dacă cifra curentă este 1, înmulțim pe A la P, P = P * A;
  • înmulțim pe A cu el însuși, A = A * A;, obținând următoarea putere din șirul de mai sus

Implementare C++:

int Putere(int A , int n)
{
    int P = 1;
    while(n)
    {
        if(n % 2 == 1)
            P = P * A;
        A = A * A;
        n /= 2;
    }
    return P;
}

altă variantă, care folosește operațiile pe biți:

int Putere(int A , int n)
{
    int P = 1;
    for(int k = 1 ; k <= n ; k <<= 1)
    {
        if((n & k))
            P *= A;
        A = A * A;
    }
    return P;
}

Observații

• ridicarea la putere rapidă poate fi folosită și pentru:
  • operații modulo (determinarea restului împărțirii rezultatului la o valoare dată)
  • numere mari
  • ridicarea la putere a matricelor
  • ridicarea la putere a polinoamelor

În numeroase probleme de informatică se cere determinarea restului împărțirii unui anumit număr (de regulă rezultat ale unui calcul) la o valoare dată, N. De cele mai multe ori numărul nu poate fi determinat direct, valoarea sa fiind prea mare. În aceste situații intervine aritmetica modulară, în care restul cerut se determină facând operații cu resturi la împărțirea cu N a unor rezultate parțiale.

Fie \( N > 1\) un număr natural și două numere întregi \(a\) și \(b\). Spunem că \(a\) și \(b\) sunt congruente modulo \(N\) , \( a \equiv b \mod N \) dacă \( N \vert (a-b) \). Echivalent, dacă \(a\) și \(b\) dau același rest la împărțirea cu \(N\).

Adunarea și înmulțirea

Avem următoarele reguli – spunem că congruența modulo N este compatibilă cu adunarea și înmulțirea numerelor întregi :

• Dacă \( a \equiv x \mod N \) și \( b \equiv y \mod N \), atunci \( a + b \equiv x + y \mod N \).
• Dacă \( a \equiv x \mod N \) și \( b \equiv y \mod N \), atunci \( a \cdot b \equiv x \cdot y \mod N \).

Consecințe (C/C++):

• având două numere naturale a, b, iar N > 1 unu număr natural:
  • restul împărțirii sumei la N este (a + b) % N = (a % N + b % N) % N
  • restul împărțirii produsului la N este (a * b) % N = ((a % N) * (b % N)) % N
• având n numere naturale A[1], A[2], …, A[n], restul împărțirii la N a produsului lor se determină astfel:

int P = 1;
for(int i =1 ; i <= n ; i ++)
    P = (P * A[i]) % N;

• pentru a calcula restul împărțirii la N a lui N! – N factorial:

int P = 1;
for(int i =1 ; i <= N ; i ++)
    P = (P * i) % N;

Scăderea

Fie numerele naturale a ≥ b și N>1. Deși congruența modulo N este compatibilă cu operația de scădere, expresia (a-b)%N = (a%N-b%N)%N nu este întotdeauna corectă.

Mai precis, chiar dacă a > b, deci (a-b)%N≥0, expresia (a%N-b%N) și deci (a%N-b%N)%N poate fi negativă. Situatia poate fi rezolvată ușor, adunând la X=(a%N-b%N)%N valoarea N, astfel X nemaifiind negativ.

Exemplu: Fie n m, două numere naturale, 1 ≤ n ≤ m ≤ 1000. Determinați restul împărțirii lui m!-n! la 1009.

Rezolvare: Fie N = 1009. Deoarece numere sunt mari, nu putem calcula factorialele. Vom calcula A = m! % N, B= n! % N, apoi X = (A-B)%N. Dacă X este negativ, vom aduna la X valoarea N, acesta fiind și rezultatul.

Următoarea secvență C++ implementează ideea de mai sus:

int n , m;
const int N = 1009;
cin >> n >> m; // n <= m
int  A = 1, B = 1;
for(int i = 1 ; i <= m ; i ++)
    A = (A * i) % N;
for(int i = 1 ; i <= n ; i ++)
    B = (B * i) % N;
int X = A - B;
if(X < 0)
    X += N;
cout << X;

Împărțirea. Inversul modular

Congruența modulo N nu este compatibilă cu împărțirea. Consecința este că (B/A) % N != ((B % N)/(A % N)) % N. Pentru a determina rezultatul modulo N al unor expresii în care intervin împărțiri vom folosi inversul modular.

Acesta permite transformarea expresiei B/A % N într-o înmulțire și poate fi determinat numai dacă numerele A și N sunt prime între ele.

Mai precis, dacă 1 ≤ A < N, inversul lui A modulo N este un număr natural 1 ≤ A-1 < N cu proprietatea că \( A \cdot A^{-1} \equiv 1 \mod N \). Atunci (B/A) % N = (B * A-1) % N = ((B%N)*(A-1%N))%N.

Există mai multe modalități de a determina inversul modular. În cele ce urmează vom nota inversul modular al lui A cu I.

O primă variantă este să analizăm fiecare număr k cuprins între 1 și N-1. Dacă A * k % N este 1, atunci I=k. Complexitatea este \(O(n)\).

Aplicând teorema lui Euler, \(A^{\varphi(N)} \equiv 1 (\mod N)\), unde \(\varphi(N)\) este indicatorul lui Euler. Atunci \(A \cdot A^{\varphi(N)-1} \equiv 1 (\mod N)\), deci \(I=A^{\varphi(N)-1} \mod N\). Acest rezultat poate fi determinat folosind exponențierea rapidă cu complexitatea \(O(\log_{2}N)\). Putem calcula indicatorul lui Euler cu complexitatea \(O(\sqrt{N})\), deci complexitatea determinării inversului modular devine \(O(\log_{2}N \cdot \sqrt{N})\).

Dacă N este prim, atunci \(\varphi(N) = N – 1\), deci \( I = A ^{N-2} \mod N\). Pentru determinare folosim exponențierea rapidă.

Cea mai eficientă metodă de a determina inversul modular folosește algoritmul lui Euclid extins, pentru A și N. Conform acestuia, există X și Y astfel încât A*X + N*Y = 1, deoarece 1=cmmdc(A,N), A și N fiind prime între ele. Trecând la operațiile modulo N, obținem \(A \cdot X \equiv 1 \mod N\), deoarece \(N \cdot Y \equiv 1 \mod N\). De aici rezultă că inversul modular al lui A modulo N este chiar X. Dacă X determinat astfel este negativ, îl vom mări cu N până când devine pozitiv.

Următoarea secvență C++ determină inversul modular al lui A, modulo N:

void euclid(int a , int b ,int & x ,int & y)
{
    if(b == 0)
    {
        x = 1, y = 1;
    }
    else
    {
        int x1 , y1;
        euclid(b , a % b , x1 , y1);
        x = y1;
        y = x1 - a / b * y1;
    }
}

int main()
{
    int A = 9, N = 11; // prime intre ele, 1 <= A < N
    int X , Y;
    euclid(A, N , X ,Y);
    while(X < 0)
        X += N;
    cout << X; // 5
    return 0;
}

Inversul modular poate fi folosit, de exemplu pentru a calcula \(C_n^k\) modulo P, unde P este un număr prim.

Algoritmul lui Euclid pentru determinarea celui mai mare divizor comun a două numere naturale are următoarea consecință: pentru două numere naturale nenule \(a\), \(b\) există numerele întregi \(x\), \(y\) astfel încât \(a \cdot x + b \cdot y = d\), unde \( d=(a,b)\) este cel mai mare divizor comun al lui \(a\) și \(b\).

Algoritmul lui Euclid

Algoritmul lui Euclid se bazează pe următoarea formulă:

\( (a,b) = \begin{cases} a& \text{dacă } b = 0\\ (b,r)& \text{dacă } b \neq 0 \end{cases} \), unde \(r\) este restul împărțirii lui \(a\) la \(b\).

Analizăm cazul \(b \neq 0\). Fie \( d=(a,b)\) Conform teoremei împărțiri cu rest, există numele naturale \(c\) și \(r\), astfel încât \( a = b \cdot c + r \), unde \( 0 \leqslant r < b\).

Dacă \( d \vert a\) și \( d \vert b \) atunc \(d \vert (a-b \cdot c)\), adică \( d \vert r\). Să presupunem că există un număr \(n > d\), astfel încât \(n = (b,r)\). Atunci \( n \vert b \) și \( n \vert r \), deci \( b \vert (b \cdot c + r) \), adică \( n \vert a \). Astfel, \( n \) este divizor comun al lui \(a\) și \(b\), dar \(d\) este cel mai mare divizor comun al lui \(a\) și \(b\) – contradicție.

Următoarea funcție recursivă implementează algoritmul lui Euclid și întoarce rezultatul printr-un parametru de ieșire:

void euclid(int a , int b ,int & d)
{
    if(b == 0)
        d = a;
    else
        euclid(b , a % b , d);
}

Algoritmul extins

Pentru a determina numere \(x\), \(y\) de mai sus, vom extinde funcția de mai sus, adăugându-i parametrii de ieșire x și y:

void euclid(int a , int b ,int & d, int & x ,int & y);

Determinarea valorilor lui x și y se va face astfel:

• dacă b este nul, atunci d = a și deoarece a * 1 + 0 * y = a, deducem că x=1, iar y poate lua orice valoare, de exemplu y=0;
• dacă b este nenul, se determină în urma autoapelului x1 și y1 astfel încât b*x1+r*y1=d, unde r = a % b. Pe de altă parte, a = b * c + r, unde c = a / b, deci r = a - b * c. Înlocuind, obținem:
  • b * x1 + (a - b * c) * y1 = d
  • b * x1 + a * y1 - b * c * y1 = d
  • a * y1 + b * (x1 - c * y1) = d, unde c = a / b – câtul impărțirii
  • a * y1 + b * (x1 - a / b * y1) = d
  • deci x = y1 și y = x1 - a / b * y1

Funcția următoare implementează algoritmul descris mai sus:

void euclid(int a , int b ,int & d, int & x ,int & y)
{
    if(b == 0)
    {
        d = a;
        x = 1, y = 1;
    }
    else
    {
        int x1 , y1;
        euclid(b , a % b , d, x1 , y1);
        x = y1;
        y = x1 - a / b * y1;
    }
}

Invers modular

Operația B/A nu poate fi realizată modulo N astfel: (B/A) % N != ((A % N)/(B % N)) % N – ușor de verificat pentru exemple concrete – deși relațiile similare au loc pentru adunare și înmulțire.

Restul împărțirii la N a lui B/A poate fi determinat, dacă A și N sunt prime între ele, prin intermediul inversului modular – dacă A și N nu sunt prime între ele, inversul modular nu există.

Mai precis, dacă 1 ≤ A < N, inversul lui A modulo N este un număr natural 1 ≤ A-1 < N cu proprietatea că \( A \cdot A^{-1} \equiv 1 \mod N \). Atunci (B/A) % N = (B * A-1) % N = ((B%N)*(A-1%N))%N.

Pentru a determina inversul modular, folosim algoritmul lui Euclid extins. Mai precis, conform algoritmului, există X și Y astfel încât A*X + N*Y = 1, deoarece 1=cmmdc(A,N), A și N fiind prime între ele. Trecând la operațiile modulo N, obtinem \(A \cdot X \equiv 1 \mod N\), deoarece \(N \cdot Y \equiv 0 \mod N\). De aici rezultă că inversul modular al lui A modulo N este chiar X. Dacă X determinat astfel este negativ, îl vom mări cu N până când devine pozitiv.

Următoarea secvență C++ determină inversul modular al lui A, modulo N:

void euclid(int a , int b ,int & x ,int & y)
{
    if(b == 0)
    {
        x = 1, y = 1;
    }
    else
    {
        int x1 , y1;
        euclid(b , a % b , x1 , y1);
        x = y1;
        y = x1 - a / b * y1;
    }
}

int main()
{
    int A = 9, N = 11; // prime intre ele, 1 <= A < N
    int X , Y;
    euclid(A, N , X ,Y);
    while(X < 0)
        X += N;
    cout << X; // 5
    return 0;
}

Inversul modular poate fi folosit, de exemplu pentru a calcula \(C_n^k\) modulo P, unde P este un număr prim.