Articole
Tare conexitate
Un graf orientat G=(V,E) este tare conex dacă pentru orice pereche de noduri distincte (x,y) există cel puțin un drum de la x la y și există cel puțin un drum de la y la x.
Pentru un graf orientat, se numește componentă tare conexă un subgraf tare conex maximal – prin adăugarea a încă unui nod, subgraful obținut nu mai este tare conex.
Exemplu

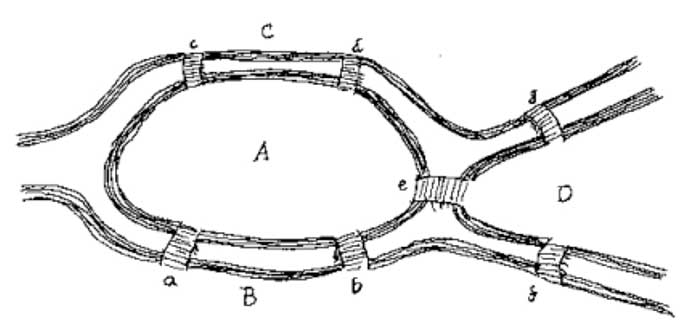
Graful de mai sus nu este tare conex. El are trei componente tare conexe.
Verificarea tare conexității. Determinarea componentelor tare conexe
Verificare tare conexității unui graf orientat poate fi privită ca un caz particular al determinării componentelor tare conexe, deoarece, dacă graful are o singură componentă tare conexă atunci el este tare conex. În continuare vom vedea două metode de determinare a componentelor tare conexe. Ambele folosesc noțiunea de graf transpus, pe care o definim în continuare:
Definiție: Fie G=(V,E) un graf orientat. Se numește graf transpus al lui G graful orientat GT=(V,ET), cu aceeași mulțimea a nodurilor și pentru orice pereche de noduri are loc: (x,y) este arc în G dacă și numai dacă (y,x) este arc în GT.
Exemplu
| Graf orientat inițial | Graful orientat transpus |
 |
 |
Să observăm că pentru două noduri oarecare x, y:
- existența unui drum de la
xlaypoate fi determinată cu o parcurgere (de exemplu în adâncime) în grafulG, pornind din nodulx; - existența unui drum de la
ylaxpoate fi determinată cu o parcurgere în grafulGT, pornind tot din nodulx.
Algoritmul Plus-Minus
Folosind observații de mai sus, pentru a determina componentele tare conexe folosim următorul algoritm, numit Plus-Minus:
- pentru fiecare nod
xal grafului care încă nu a fost plasat într-o componentă tare conexă:- determinăm toate nodurile în care se poate ajunge din
x, folosind grafulGși le marcăm într-un tablou cu plus; - determinăm toate nodurile din care se poate ajunge în
x, folosind grafulGTși le marcăm într-un tablou cu minus; - nodurile marcate atât cu plus, cât și cu minus, împreună cu
xformează o componentă tare conexă;
- determinăm toate nodurile în care se poate ajunge din
Exemplu:
Fie graful de mai sus. Să determinăm componenta tare conexă din care face parte nodul 6:
| Graful inițial | Graful transpus |
 |
 |
S-au marcat cu plus nodurile: 5 7 8 |
S-au marcat cu minus nodurile: 1 2 3 4 5 7 8 |
Nodurile marcate de două ori, 5 7 8, împreună cu nodul inițial, 6, formează o componentă tare conexă.
Secvență C++:
n, a[][]– numărul de noduri și matricea de adiacențănrc– numărul de componente tare conexectc[]– tablou pentru memorarea componentelor tare conexe:ctc[i] =numărul de ordine al componentei din care face parte nodulis[], p[]– tablouri pentru marcarea nodurilor vizitate în timpul parcurgerilor- să observăm că graful inițial și cel transpus pot fi memorate prin aceeași matrice de adiacență
void df1(int x)
{
s[x] = 1;
for(int i =1 ; i <= n ; i ++)
if(s[i] == 0 && a[x][i] == 1)
df1(i);
}
void df2(int x)
{
p[x] = 1;
for(int i =1 ; i <= n ; i ++)
if(p[i] == 0 && a[i][x] == 1)
df2(i);
}
int main()
{
.....
for(int i = 1 ; i <= n ; ++i)
if(ctc[i] == 0)
{
for(int j = 1; j <= n ; ++j)
s[j] = p[j] = 0;
nrc ++;
df1(i); df2(i);
for(int j = 1; j <= n ; ++j)
if(s[j] == 1 && p[j] == 1)
ctc[j] = nrc;
}
....
}
Algoritmul lui Kosaraju
Alt algoritm, mai eficient, pentru determinarea componentelor tare conexe este Algoritmul lui Kosaraju.
Să ne amintim că la parcurgerea în adâncime se pot asocia nodurilor două momente de timp:
d[x]– momentul când nodulxeste descoperit și adăugat pe stivă: timpul de descoperire a noduluif[x]– momentul când se termină de vizitat succesorii luix, iar nodulxse elimină de pe stivă: timpul de finalizare a nodului
Aceste momente de timp vor fi numere naturale între 1 și 2*n, unde n este numărul de noduri din graf.
Algoritmul lui Kosaraju este:
- determinăm graful transpus
GT - parcurgem în adâncime graful și determinăm pentru fiecare nod
xtimpul de finalizaref[x] - parcurgem în adâncime graful transpus
GT, dar considerăm nodurile în ordinea descrescătoarea timpilor de finalizare - nodurile din arborii de parcurgere obținuți reprezintă câte o componentă tare conexă
Exemplu:
| Graf orientat inițial | Graful orientat transpus |
 |
 |
În urma parcurgerii în adâncime a grafului inițial G nodurile în ordinea finalizării sunt: 
Parcurgem graful transpus GT analizând nodurile în ordinea inversă a timpilor de finalizare:
- începem cu nodul
1; se vizitează nodurile3 4; se determină componenta tare conexă{1,3,4}; - continuăm cu nodul
2(nodurile1,3și4au fost vizitate mai devreme); nu se vizitează alte noduri; se determină componenta tare conexă{2}; - continuăm cu nodul
5; se vizitează nodurile6 8 7; se determină componenta tare conexă{5, 6, 7, 8}.

Secvență C++:
#include <iostream>
#include <fstream>
#include <vector>
using namespace std;
vector<vector<int> > G, GT;
int n , m , contor , nrs;
vector<bool> V;
vector<int> S;
void read()
{
cin >> n >> m;
G = GT = vector<vector<int>>(n + 1);
for(int i = 1 ; i <= m ; i++)
{
int a , b;
cin >> a >> b;
G[a].push_back(b);
GT[b].push_back(a);
}
}
void dfs(int k)
{
V[k] = true;
for(auto x : G[k])
if(!V[x])
dfs(x);
S.push_back(k);
}
void dfsGT(int k)
{
V[k]=1;
for(auto x: GT[k])
if(! V[x])
dfsGT(x);
}
int main()
{
read();
V = vector<bool> (n + 1, false);
for(int i = 1 ; i <= n ; i ++)
if(! V[i])
dfs(i);
V = vector<bool> (n + 1, false);
for(vector<int>::reverse_iterator it = S.rbegin() ; it != S.rend() ; it ++)
if(!V[*it]) {
contor ++;
dfsGT(*it);
}
cout<<contor;
return 0;
}
Complexitatea acestui algoritm este aceea a parcurgerii în adâncime: O(n2) dacă memorăm graful prin matricea de adiacență, O(n+m) dacă memorăm graful prin liste de adiacență.
Algoritmul Roy-Warshall-Floyd
În jurul anului 1960 a fost descoperit un algoritm pentru drumuri în grafuri orientate. Descoperirea a fost făcută independent de către trei oameni de stiință în domeniul algoritmilor: Robert Floyd, Bernard Roy și Stephen Warshall.

Algoritmul se regăsește sub diferite denumiri care conțin numele descoperitorilor, este bazat pe programarea dinamică și poate fi utilizat în următoarele două moduri:
- pentru un graf orientat oarecare determină matricea drumurilor – stabilește despre oricare două noduri
x ydacă există drum de laxlay– este de regulă cunoscut sub numele Roy-Warshal - pentru un graf orientat ponderat (cu costuri) – determină pentru fiecare pereche de noduri costul minim al unui drum cu extremitățile în acele noduri – este de regulă cunoscut sub numele Roy-Floyd
Ambele variante permit și reconstituirea unor drumuri între două noduri date.
Graf eulerian
În 1736, matematicianul elvețian Leonard Euler a rezolvat o problemă cunoscută astăzi ca “Problema celor șapte poduri din Königsberg”. Prin orașul Königsberg, azi Kaliningrad trece un râu pe care sunt două insule, acestea și malurile fiind unite prin poduri ca în imaginea de mai jos.
Leonard Euler a demonstrat că nu este posibil ca o persoană să traverseze fiecare pod o singură dată. În onoarea sa, o categorie specială de grafuri se numesc grafuri euleriene.
Definiții:
- Într-un graf neorientat, se numește lanț eulerian un lanț simplu în care apare fiecare muchie (fiind lanț simplu, fiecare muchie apare o singură dată).
- Într-un graf neorientat, se numește ciclu eulerian un ciclu în care apare fiecare muchie.
- Un graf neorientat se numește graf eulerian dacă conține un ciclu eulerian.
Exemplu:

În graful de mai sus ciclul (1 2 4 5 3 6 5 2 3 1) este eulerian.
Teoremă:
Un graf neorientat fără vârfuri izolate este eulerian dacă și numai dacă este conex și toate vârfurile au grad par.
Un graf neorientat fără vârfuri izolate conține un lanț eulerian, dacă și numai dacă este conex și toate vârfurile au grad par, mai puțin două. Aceste vârfuri vor fi extremitățile lanțului eulerian.
Pentru determinarea unui ciclu eulerian se pot folosi mai mulți algoritmi. Unul dintre aceștia este asemănător cu parcurgerea în adâncime. Vom folosi o stivă (eventual memoria STACK prin intermediul recursivității):
- adăugăm pe stivă un vârf oarecare – de exemplu
1; - cât timp stiva nu este vidă
- fie
k– nodul din vârful stivei - determinăm nodurile
xadiacente cuk. Eliminăm muchia[k,x]și adăugăm nodulxpe stivă (apel recursiv)- continuăm cu nodul situat în vârful stivei
- adăugăm nodul
kîntr-o listă - eliminăm nodul
kdin stivă
- fie
- lista construită reprezintă ciclu eulerian
Important:
- la vizitarea unui vârf, acesta nu va fi marcat, pentru a permite revenirea în el;
- finitudinea algoritmului este asigurată de faptul că muchiile se elimină din graf;
Secvență C++:
Considerăm un graf cu n vârfuri, memorat prin intermediul matricei de adiacență, A[][]. Tabloul L[] reprezintă lista în care se memorează ciclul eulerian. Toate variabilele sunt globale:
void Euler(int k)
{
for(int i = 1 ; i <= n ; i ++)
if(A[k][i] == 1)
{
A[k][i] = A[i][k] = 0;
Euler(i);
}
L[++p] = k;
}
...
Euler(1);
...
Algoritmul de mai sus poate fi utilizat și pentru determinarea unui lanț eulerian. Parcurgerea trebuie să înceapă însă din unul dintre vârfurile cu grad impar.
Graf hamiltonian
Problema comis voiajorului este o problemă celebră de informatică: Un comis-voiajor (agent comercial) trebuie să viziteze n orașe. Cunoscându-se șoselele existente între orașe, să se determine o modalitate (toate modalitățile) prin care comis-voiajorul poate parcurge fiecare oraș o singură dată și se întoarce în orașul de plecare.
Dacă asociem problemei un graf neorientat, constatăm că trebuie să determinăm un ciclu elementar (toate ciclurile elementare) care trece prin toate vârfurile grafului. Un astfel de ciclu se numește ciclu hamiltonian.
Definiții:
- Într-un graf neorientat, se numește lanț hamiltonian un lanț elementar care conține toate vârfurile grafului.
- Într-un graf neorientat, se numește ciclu hamiltonian un ciclu elementar care conține toate vârfurile grafului.
- Un graf neorientat se numește graf hamiltonian dacă conține un ciclu hamiltonian.
Pentru un graf orientat se pot definii noțiuni similare, de drum hamiltonian și circuit hamiltonian
Exemplu:

În graful de mai sus sunt evidențiate muchiile care fac parte dintr-un ciclu hamiltonian: (1, 2, 5, 4, 6, 3).
În anumite condiții se poate stabili că un graf dat este hamiltonian. Dar aceste condiții sunt “de suficiență”. Dacă nu sunt îndeplinite, nu înseamnă că graful nu este hamiltonian!
Teoreme:
- Fie
G=(X,U)un graf neorientat cu \( n \) vârfuri și un lanț hamiltonian \( v_1, v_2, \cdots, v_n \). Dacă \( d(v_1) + d(v_n) \geq n\), atunci graful este hamiltonian, unde \( d(x) \) este gradul vârfului \(x \). - Fie
G=(X,U)un graf neorientat cu \( n \) vârfuri. Dacă pentru orice pereche de vârfuri neadiacente distincte \( v_i, v_j \) avem relația \( d(v_i) + d(v_j) \geq n\), atunci graful este hamiltonian. - Un graf neorientat în care gradul fiecărui vârf este mai mare sau egal cu jumătate din numărul de vârfuri este hamiltonian.
- Un graf complet cu \(n > 2\) vârfuri conține \(\frac{(n-1)!}{2}\) cicluri hamiltoniene.
Vectori caracteristici și de frecvență
Considerăm următoarea problemă: Se dau două șiruri de cifre zecimale. Să se determine cifrele comune, în ordine crescătoare.
În funcție de numărul de cifre din cele două șiruri, putem realiza diverse soluții:
- căutăm fiecare termen din primul șir în al doilea șir. Șirul cu valorile comune va trebui sortat.
- dacă șirurile sunt sortate (sau le sortăm) procedăm ca mai sus, dar căutăm binar. Șirul cu valorile comune este de la început sortat.
- dacă șirurile sunt sortate (sau le sortăm) putem folosi interclasarea pentru a afla elementele comune.
Vector caracteristic
Nicio soluție dintre cele de mai sus nu ține cont de o proprietate a valorilor din șir – că sunt cifre, adică între 0 și 9. Putem proceda astfel:
- pentru fiecare șir vom folosi un vector cu doar
10elemente, indexate de la0la9; fie acesteav[]șiu[]; - indicii elementelor din șir reprezintă cifrele – valorile posibile ale elementelor din șir;
- inițial elementele celor doi vectori sunt
0; - pentru fiecare valoare
x(care este cifră) care apare în primul șir vom marca în vectorulv[]elementul corespunzător cu1,v[x] = 1; - similar, fiecare element
ydin al doilea șir va fi marcat în vectorulu[]cu1,u[y] = 1; - la final sunt comune cifrele
c(de la0la9) care sunt marcate cu1atât în vectorulv[], cât și în vectorulu[].
Cei doi vectori v[] și u[] sunt vectori caracteristici. Elementele lor caracterizează cifrele dintre 0 și 9, stabilind despre fiecare cifră dacă face sau nu parte din șirul corespunzător.
Observăm că nu trebuie memorate elementele celor două șiruri date. Ne interesează numai valorile distincte care apar în fiecare șir, indiferent de ordinea în care apar.
Exemplu:

Observații:
- vectorul caracteristic are dimensiune constantă – egală cu numărul de valori pe care le caracterizează;
- elementele vectorului caracteristic sunt
0sau1(echivalent cu Adevărat și Fals); valorile din vectorul caracteristic NU sunt valorile date; - valorile date se află printre indicii vectorului caracteristic, respectiv indicii corespunzători elementelor egale cu
1;
Când folosim vectorul caracteristic?
Pentru a putea folosi un vector caracteristic trebuie îndeplinite (cel puțin) următoarele condiții:
- ordinea datelor de intrare nu contează
- datele de intrare au valori mici, sunt numere naturale dintr-un interval de forma
[0,M]sau pot fi echivalente cu astfel de numere - practic, putem folosi un vector caracteristic dacă memoria disponibilă permite declararea unui vector cu un număr de elemente corespunzător:
- dacă datele de intrare sunt din intervalul
[0, 1000]sau[0,10000]putem folosi un vector caracteristic - dacă datele de intrare sunt din intervalul
[0, 1 milion]putem folosi un vector caracteristic – deși poate există metodă mai bună - dacă datele de intrare sunt din intervalul
[0, 1 miliard]NU putem folosi un vector caracteristic
- dacă datele de intrare sunt din intervalul
Vector de frecvență
Să considerăm din nou un șir de cifre zecimale. Să se determine cifra care apare de cele mai multe ori. Dacă sunt mai multe cifre care apar de număr maxim de ori, să se determine cea mai mică (sau cea mai mare, sau toate, etc.).
De această dată nu putem folosi un vector caracteristic, dar putem folosi un vector de frecvență, adică un vector cu același număr de elemente ca numărul posibil de valori distincte din șirul dat (adică 10), cu semnificația: v[c] = numărul de apariții ale cifrei c în șirul dat.
După construirea acestui vector, valoarea maximă din el va reprezenta numărul maxim de apariții ale unei cifre, iar indicii pentru care elementul corespunzător are valoare maximă reprezintă cifrele care apar de număr maxim de ori.
Exemplu:

Sume parțiale în tablouri
Considerăm un tablou cu elemente numerice. În unele probleme se cere să determinăm rapid suma elementelor din anumite secvențe date. Desigur, o soluție este parcurgerea tuturor elementelor din secvență și determinarea sumei, dar această operație are complexitatea \( O(n) \), iar dacă numărul de sume care trebuie calculate este mare soluția poate fi inacceptabilă.
În asemenea situații putem folosi sumele parțiale.
Reamintim că se numește secvență a vectorului X o succesiune de elemente consecutive din X, în ordinea din X. Mai multe detalii sunt disponibile aici.
Sume parțiale în vectori
Fie un vector X[] cu n elemente. Pentru simplitate vom considera că elementele sunt indexate de la 1 la n.

Să determinăm suma elementelor din secvența determinată de indicii 4 7:

Valoarea sumei este X[4] + X[5] + X[6] + X[7] = 8 + 1 + 3 + 0 = 12.
Pentru a determina rapid această sumă, vom construi un vector auxiliar, \( S[] \), cu următoarea semnificație: \( S[i]=X[1]+X[2]+...+X[i] \). Acest vector se construiește în timp liniar, folosind următoarea relație de recurență:
$$ S[i] = \begin{cases}
0& \text{dacă } i = 0,\\
S[i-1] + X[i] & \text{dacă } i > 0.
\end{cases} $$

pentru a determina suma elementelor din secvența determinată de indicii i j folosim următoarea formulă, în timp constant:
$$ X[i] + X[i+1] + ... + X[j] = S[j] - S[i-1] $$

Astfel:
$$ \begin{split} X[4] + X[5] + X[6] + X[7] & = S[7] - S[3] \\ & = 28 - 16 \\ & = 12 \end{split} $$
Observație: Este posibil ca suma elementelor din vectorul X[] să depășească limita maximă a tipului de date folosit (ex. int), ceea ce duce la overflow. În acest caz, vectorul S[] trebuie declarat de un tip mai larg (ex. long long int).
Secvență C++
int n, X[100001], S[100001];
//citire n, X[]
S[0] = 0;
for(int i = 1 ; i <= n ; i ++)
S[i] = S[i-1] + X[i];
int st, dr; // capetele secvenței
//citire st,dr
cout << S[dr] - S[st-1];
Sume parțiale în matrice
Observațiile de mai sus pot fi extinse pentru a calcula suma elementelor dintr-o submatrice a unei matrice date A[][], cu n linii și m coloane:

Pentru matricea de mai sus, să calculăm suma elementelor din submatricea cu colțul stânga-sus la coordonatele (2,3) și colțul dreapta-jos la coordonatele (3,5). La fel ca în cazul vectorilor, considerăm, pentru simplitate, că liniile și coloanele matricei sunt indexate de la 1.
Parcurgerea element cu element a submatricei are complexitate \( O(n \cdot m) \). Pentru o complexitate constantă considerăm matricea S[][] a sumelor parțiale, astfel:
S[i][j]– suma elementelor din submatricea cu colțul stânga-sus la coordonatele(1,1)și colțul dreapta-jos la coordonatele(i,j). Elementele de pe linia0și coloana0vor avea valoarea0:

Odată construită această matrice, pentru determinarea sumei elementelor din submatricea cu colțul stânga-sus la coordonatele (is,js) și colțul dreapta-jos la coordonatele (ij,jj) vom folosi următoarea formulă:
Suma(is,js,ij,jj) = S[ij][jj] - S[is-1][jj] - S[ij][js-1] + S[is-1][js-1]
 |
 |
Matricea S[][] se construiește similar cu modul în care se determină suma din submatrice:
$$ S[i][j] = \begin{cases}
0& \text{dacă } i = 0 \text{ sau } j = 0,\\
S[i-1][j] + S[i][j-1] – S[i-1][j-1] + A[i][j] & \text{dacă } i > 0 \text{ și } j > 0.
\end{cases} $$
Observație: Este posibil ca suma elementelor din matricea dată să depășească limita maximă a tipului de date folosit (ex. int), ceea ce duce la overflow. În acest caz, matricea S[][] trebuie declarată de un tip mai larg (ex. long long int).
Secvență C++
int n,m, A[1001][1001], S[1001][1001];
//citire n,m,A[][]
for(int i = 0 ; i <= n ; i ++)
S[i][0] = 0;
for(int j = 0 ; j <= m ; j ++)
S[0][j] = 0;
for(int i = 1 ; i <= n ; i ++)
for(int j = 1 ; j <= m ; j ++)
S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j];
int is,js; // coltul stanga sus
int ij,jj; // coltul dreapta jos
//citire is,js, ij,jj;
cout << S[ij][jj] - S[is-1][jj] - S[ij][js-1] + S[is-1][js-1];Căutarea binară
Introducere
Căutarea unei valori într-un vector se poate face în două moduri:
- secvențial – presupune analizarea fiecărui element al vectorului într-o anumită ordine (de obicei de la stânga la dreapta). Când se găsește valoarea căutată parcurgerea vectorului se poate opri. În cel mai rău caz, pentru un vector cu
nelemente parcurgerea facenpași, complexitatea timp a căutării secvențiale esteO(n) - binar. Căutarea binară se poate face într-un vector numai dacă elementele acestuia sunt în ordine (de obicei crescătoare) după un anumit criteriu (de obicei criteriul este chiar relația de ordine naturală între numere, cuvinte, etc). Căutarea binară presupune împărțirea vectorului în secvențe din ce în ce mai mici, înjumătățindu-le și continuând cu jumătatea în care se poate afla valoarea dorită (conform ordinii elementelor din vector).
Algoritm pseudocod
Algoritmul căutării binare este următorul:
Date de intrare:
- un vector
v[]cunelemente, indexate de la1lan, ordonate crescător și o valoarexcare se va căuta.
Date de ieșire:
- un indice
pozdacă valoareaxapare în vectorulv[]sau0în caz contrar.
Algoritm pseudocod:
st ← 1
dr ← n
poz ← 0
CÂTTIMP st≤dr SI poz=0 EXECUTĂ
m ← (st + dr) DIV 2
DACĂ v[m] = x ATUNCI
poz = m
ALTFEL
DACĂ v[m] < x ATUNCI
st ← m + 1
ALTFEL
dr ← m - 1
SFDACĂ
SFDACĂ
SFCÂTTIMP
DACĂ poz≠0 ATUNCI
// x apare în vector pe poziția poz
ALTFEL
// x nu apare în vector
SFDACĂ
Notă: În algoritmul de mai sus a DIV b reprezintă câtul împărțirii lui a la b, iar cu V ← EXPR s-a notat atribuirea la variabila V a rezultatului expresiei EXPR.
Altă variantă a căutării binare
De multe ori nu este suficient să știm dacă o valoare dată apare sau nu în vector. Sunt numeroase situații în care trebuie să aflăm un indice al vectorului (element al vectorului) care respectă o anumită condiție în raport cu valoarea dată. De exemplu:
- să se determine cel mai mare indice
pozpentru carev[poz] ≤ x; - să se determine cel mai mare indice
pozpentru carev[poz] < x; - etc.
Algoritmul de mai jos determină cel mai mare indice poz pentru care v[poz] ≤ x. El poate fi folosit și pentru a verifica dacă x apare în vector, astfel: dacă la final v[poz] = x, atunci x apare în vector, in caz contrar nu apare.
st ← 1
dr ← n
poz ← n + 1
CÂTTIMP st ≤ dr EXECUTĂ
m ← (st + dr) DIV 2
DACĂ v[m] ≥ x ATUNCI
poz ← m
dr ← m - 1
ALTFEL
st ← m + 1
SFDACĂ
SFCÂTTIMP
DACĂ v[poz] = x ATUNCI
// x apare în șir pe poziția poz
ALTFEL
// x nu apare în șir (în acest caz, v[poz] > x)
SFDACĂȘmenul lui Mars - Difference Array
Șmenul lui Mars în vector
Să presupunem că avem un vector A[] cu n elemente, indexate de la 1 la n, inițial nule, în care se fac mai multe operații Adună(s,d,X) prin care toate elementele din secvența delimitată de indicii s d cresc cu valoarea X. Se cere afișarea elementelor din A după efectuarea acestor operații.
Metoda descrisă în continuare este cunoscută în lumea olimpicilor la informatică sub numele de “Șmenul lui Mars”, atribuită fostului olimpic Marius Andrei. De asemenea, se regăsește sub numele “Difference Array”, de exemplu pe www.geeksforgeeks.org. Vezi Șmenul lui Mars pe infoarena.ro!
Operațiile pot fi efectuate eficient construind un vector suplimentar B[], cu n+1 elemente, astfel încât A[i]=B[1]+B[2]+...+B[i]. Vectorul A[] este vector de sume parțiale pentru vectorul B[].
Operația Adună(s,d,X) devine:
B[s] += X; B[d+1] -= X;
La final, elementele lui A se reconstituie astfel: A[i]=B[1]+B[2]+...+B[i]
A[1] = B[1];
for(int i = 2 ; i <= n ; i ++)
A[i] = A[i-1] + B[i];
Șmenul lui Mars în matrice
Cunoscută și sub denumirea de Șmenul lui Mars 2D, această tehnica se aplică în rezolvarea problemelor la care se cere, pentru o matrice dată A[][] mărirea cu o valoare dată X a tuturor elementelor din submatricea determinată de colțul stânga-sus (i1,j1) și colțul dreapta-jos (i2,j2). Această operație se aplică de mai multe ori, pentru diverse submatrice și diverse valori ale lui X și se cere determinarea elementelor din A[][] după aceste operații.
Putem proceda similar ca în cazul unidimensional, construind o matrice suplimentară M[][], astfel incât matricea A[][] reprezintă matrice de sume parțiale pentru M[][].
Operațiile date devin:
M[i1][j1] += x; M[i1][j2+1] -= x; M[i2+1][j1] -= x; M[i2+1][j2+1] += x;
Observații:
- Matricea
M[][]are cu o linie și o coloană mai mult decât matriceaA[][]. - Fiecare operație prin care se măresc elementele dintr-o submatrice are complexitate constantă.
Exemplu

Refacerea matricei A[][] se face ținnând cont de faptul că este matrice de sume parțiale pentru M[][]:
for(int i = 1 ; i <= n ; i ++) for(int j = 1; j <= m ; j ++) A[i][j] = M[i][j] + A[i-1][j] + A[i][j-1] - A[i-1][j-1];
Ciurul lui Eratostene
Introducere
Ciurul lui Eratostene reprezintă o metodă de determinare a tuturor numerelor prime mai mici sau egale cu o valoare dată, n. În practică, valoarea lui n trebuie să fie una rezonabilă, ea depinzând de restricțiile de timp și memorie aplicate problemei.
Ciurului Eratostene se aplică în felul următor – în continuare lucrăm cu n=30:
- se scriu toate numerele naturale de la
1lan=30:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- se taie din lista numărul
1, care nu este prim
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- se identifică următorul număr netăiat,
2. Acest este prim, iar din listă se vor tăia toți multipli săi, mai mari decât acesta.
| 2 | 3 | 5 | 7 | 9 | |||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 27 | 29 |
- se identifică următorul număr netăiat,
3. Acest este prim, iar din listă se vor tăia toți multipli săi, mai mari decât acesta. Unii dintre ei au fost deja tăiați, deoarece sunt și multipli ai lui2.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 25 | 29 |
- se identifică următorul număr netăiat,
5. Acest este prim, iar din listă se vor tăia toți multipli săi, mai mari decât acesta. Unii dintre ei au fost deja tăiați, deoarece sunt și multipli ai lui2sau3.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 |
- se identifică următorul număr netăiat,
7. Acesta este prim, dar totodată7*7>30căutarea numerelor prime s-a încheiat. Toate numerele care nu au fost tăiate sunt prime.
Animație
Algoritm
Pentru identificarea numerelor prime într-un algoritm/program, vom folosi un vector caracteristic, v[], cu următoarea semnificație:
\( v[x]=\begin{cases} 0& \text{dacă $x$ prim},\\1& \text{dacă $x$ nu este prim}.\end{cases} \)
Vom porni de la un vector cu toate elementele nule, apoi vom marca pe rând cu 1 toate numerele care sunt multipli ai unor numere mai mici. Un algoritm pseudocod care realizează acest operații este:
pentru i←0,n execută
V[i] ← 0
sf_pentru
V[0] ← 1
V[1] ← 1
pentru i ← 2,sqrt(n) execută
dacă V[i] = 0 atunci
pentru j ← 2, [n/i] execută
V[i*j] ← 1
sf_pentru
sf_dacă
sf_pentru
Probleme similare
Mecanismul prin care se identifică numerele prime specific Ciurului lui Eraostene poate fi folosit și la determinarea altor rezultate. De exemplu, vrem să aflăm pentru un n dat (nu prea mare) câți divizori are fiecare număr natural din intervalul [1,n].
Pentru acesta, vom construi un vector V, în care v[x] reprezintă numărul de divizori ai lui x. Pentru a construi acest vector, vom parcurge numerele de la 1 la n, și pentru fiecare număr x vom identifica multiplii săi. Pentru fiecare y multiplu al lui x vom incrementa valoarea lui v[y].
Un algoritm pseudocod este:
pentru i←1,n execută
V[i] ← 0
sf_pentru
pentru x ← 1,n execută
pentru y ← x, n , x execută
V[y] ← V[y] + 1
sf_pentru
sf_pentru

Generarea submulțimilor
Problema:
Se dă un număr natural
n. Să se genereze toate submulțimile mulțimii{1,2,3,...,n}.
Soluție:
Pentru rezolvare folosim metoda backtracking. Acest articol prezintă două metode de rezolvare.
Metoda 1
În vectorul soluție x[] vom memora pe rând câte o submulțime. Deoarece submulțimile au număr variabil de elemente, și vectorul soluție va avea un număr variabil de elemente.
- semnificaţia vectorului soluție:
x[]reprezintă la un moment dat o submulțime - condiții externe:
x[k]în{1,2,..,n},kîntre1șin; - condiții interne:
x[k]>x[i],iîntre1șik-1. Deoarece condițiile interne se aplică pentru toate elementele vectorului soluție, este suficient cax[k]>x[k-1], pentruk>1; - condiții de existența a soluției: fiecare variantă a vectorului soluție corespunde cu o submulțime. Orice valoare validă plasată în vectorul soluție conduce la o soluție.
void afis(int k){
for(int i=1 ; i<=k ; ++i)
cout << x[i] << " ";
cout << endl;
}
bool valid(int k){
if(k == 1)
return true;
if(x[k] > x[k-1])
return true;
return false;
}
void back(int k){
for(int i=1;i<=n;++i)
{
x[k]=i;
if(valid(k))
{
afis(k);
back(k+1);
}
}
}
Constatăm că putem rafina condițiile externe; deoarece x[k]>x[k-1], condițiile devin:
- Condiții externe:
x[k]în{x[k-1]+1, ... , n},kîntre1șin. Pentru a uniformiza algoritmul, considerăm de la început căx[0] = 0; - Condiții interne: nu mai avem condiții interne; funcția
valid()nu mai este necesară; - Condiții de existența a soluției rămân aceleași.
void back(int k){
for(int i=x[k-1]+1;i<=n;++i)
{
x[k]=i;
afis(k);
back(k+1);
}
}
Să observăm că submulțimea vidă nu se regăsește printre soluțiile generate cu acest algoritm. Dacă este cazul, afișarea ei se poate face în afara algoritmului de generare.
Metoda 2
Această metodă se bazează pe observația că pentru fiecare submulțime a mulțimii date, {1,2,...,n} îi corespunde un șir de n biți, notat x[], astfel:
- dacă bitul
x[k] = 0, elementulknu aparține submulțimii curente; - dacă bitul
x[k] = 1, elementulkaparține submulțimii curente.
Reamintim că o mulțime cu n elemente are 2 n submulțimi.
Exemplificăm cu mulțimea {1,2,3,4}.
0 |
0000 |
{} |
8 |
1000 |
{1} |
1 |
0001 |
{4} |
9 |
1001 |
{1,4} |
2 |
0010 |
{3} |
10 |
1010 |
{1,3} |
3 |
0011 |
{3,4} |
11 |
1011 |
{1,3,4} |
4 |
0100 |
{2} |
12 |
1100 |
{1,2} |
5 |
0101 |
{2,4} |
13 |
1101 |
{1,2,4} |
6 |
0110 |
{2,3} |
14 |
1110 |
{1,2,3} |
7 |
0111 |
{2,3,4} |
15 |
1111 |
{1,2,3,4} |
Putem să generăm toate șirurile de n biți, iar pentru fiecare șir să construim submulțimea corespunzătoare. Generarea șirurilor se poate face în mai multe moduri:
- parcurgem numerele de la
0la2n-1și transformăm fiecare număr în baza2; obținem astfel pentru fiecare număr un șir de biți care va fi transformat în submulțime; - generăm direct șirul de biți cerut cu metoda backtracking.
Vom detalia mai jos rezolvarea cu backtracking:
- semnificaţia vectorului soluție:
x[]conține la un moment dat un șir de biți care va corespunde unei submulțimi - condiții externe:
x[k] = 0sau1; - condiții interne nu există. Orice configurație parțială a vectorului
x[]va conduce la o soluție validă - condiții de existență a soluției:
k == n.
void afis(int k){
for(int i=1 ; i <= k ; ++i)
if(x[i] == 1)
cout << i << " ";
cout << endl;
}
void back(int k){
for(int i = 0; i <= 1 ; ++i)
{
x[k]=i;
if(k == n)
afis(k);
else
back(k+1);
}
}
Probleme
SubmDiv Submultimi Siruri