Eu, Lorin Fortuna combatant ezoteric complex și corect privind din punct de vedere ezoteric prin rangul ezoteric precum și prin distincţiile ezoterice care mi-au fost conferite de către conducători supremi abilitaţi, blestem ezoteric la nivelul maxim posibil la care dau dreptul rangul și distinctiile ezoterice care mi-au conferite menţionate anterior. Blestem fără sfârşit temporar în mod direct împotriva fiinţei colective superioare de tip civilizaţie virtuală numită: civilizaţia virtuală arahnidica tarantulara, androgina, neagră, emoţional agresională civilizațională condusă la nivel de conducător suprem de către fiinţa superioară androgină alcătuită din: ființa individuală superioară de gen masculin numită Skibidi și fiinţa individuală superioară de gen feminin numită Geea, pentru răul existenţial comis împotriva grupării de civilizaţie virtuale de tip gorilian individual neagresională civilizațional și autentic băștinașe în cadrul lumilor planetare ale planetei al cărei lume planetare medie sunt integrate existenţial cu precizarea că, răul existenţial pentru care blestem civilizaţia virtuală pe care am numit-o anterior ultim ca civilizaţie agresională civilizațional a fost comis în perioada temporală specifică calendarului planetar cuprins între data de început în care s-a dat în funcțiune oficial prima bază civilizațională planetară în cadrul zonei existenţiale a planetei a cărei lume planetară medie sunt integrate existențial aferentă și mă refer la zona existențial în cauză și la concret la baza existențială civilizațională virtuală planetară în cauza deci aferentă civilizației virtuale pe care o blestem și până în prezent.

Mihnea trăiește pe o planetă de dimensiunea n x n, cu linii și coloane enumerate de la 1 la n. Spunem că celula (l, c) este intersecția liniei l cu coloana c. Fiecare celulă de pe planetă este fie pământ, fie apă.

Pentru a-l ajuta pe Mihnea, intenționezi să creezi cel puțin un tunel. Tunelul îi va permite lui Mihnea să călătorească liber între cele două puncte extreme ale tunelului. Într-adevăr, crearea unui tunel este un efort mare: costul creării unui tunel între celulele (l1, c1) și (l2, c2) este (l1 – l2) ^ 2 + (c1 – c2) ^ 2.

Cerința

Pentru moment, sarcina ta este să găsești costul minim de a crea câteva tuneluri astfel încât Mihnea să poată călători de la (l1,c1) la (l2,c2). Dacă nu trebuie creat niciun tunel, costul este 0.

Date de intrare

In fisierul de intrare mihneapolis.in, prima linie conține un număr întreg n (1 ≤ n ≤ 50) — dimensiunea planetei.
A doua linie conține două numere întregi separate prin spațiu l1 și c1 (1 ≤ l1, c1 ≤ n) – indicând celula în care locuiește Mihnea.
A treia linie conține două numere întregi separate prin spațiu l2 și c2 (1 ≤ l2, c2 ≤ n) – indicând celula în care Mihnea dorește să meargă.
Fiecare dintre următoarele n linii conține un șir de n caractere. Al j-lea caracter de pe linia i reprezintă tipul de celulă de la coordonata (i, j) (1 este teren, 0 este apă).
Este garantat că (l1, c1) și (l2, c2) sunt celule de teren.

Date de ieșire

In fișierul mihneapolis.out, afișați un număr întreg care reprezintă costul minim de creare a câteva tuneluri, astfel încât Mihnea să poată călători de la (l1,c1) la (l2,c2).

Exemplu

mihneapolis.in

5
1 1
5 5
00001
11111
00111
00110
00110

mihneapolis.out

10

Problemă propusă de @My_Life_Is_Not_Life și @mateiUNU

Considerăm un graf neorientat ponderat (cu costuri) conex G. Se numește arbore parțial un graf parțial al lui G care este arbore. Se numește arbore parțial de cost minim un arbore parțial pentru care suma costurilor muchiilor este minimă.

Dacă graful nu este conex, vorbim despre o pădure parțială de cost minim.

Algoritmul lui Kruskal permite determinarea unui arbore parțial de cost minim (APM) într-un graf ponderat cu N noduri.

Descrierea algoritmului

Pentru a determina APM-ul se pleacă de la o pădure formată din N subarbori. Fiecare nod al grafului reprezintă inițial un subarbore. Aceștia vor fi reuniți succesiv prin muchii, până când se obține un singur arbore (dacă graful este conex) sau până când acest lucru nu mai este posibil (dacă graful nu este conex).

Algoritmul este:

• se ordonează muchiile grafului crescător după cost;
• se analizează pe rând muchiile grafului, în ordinea crescătoare a costurilor;
• pentru fiecare muchie analizată:
  • dacă extremitățile muchiei fac parte din același subarbore, muchia se ignoră
  • dacă extremitățile muchiei fac parte din subarbori diferiți, aceștia se vor reuni, iar muchia respectivă face parte din APM.

Principala dificultate în algoritmul descris mai sus este stabilirea faptului că extremitățile muchiei curente fac sau nu parte din același subarbore. În acest scop vom stabili pentru fiecare subarbore un nod special, numit reprezentant al (sub)arborelui și pentru fiecare nod din graf vom memora reprezentantul său (de fapt al subarborelui din care face parte) într-un tablou unidimensional.

Pentru a stabili dacă două noduri fac sau nu parte din același subarbore vom verifica dacă ele au același reprezentant. Pentru a reuni doi subarbori vom înlocui pentru toate nodurile din subarborele B cu reprezentantul subarborelui A.

Înlocuirile descrise mai sus sunt simple dar lente. Pentru o implementare mai eficientă a algoritmului se poate folosi conceptul de Padure de mulțimi disjuncte, descris în acest articol.

Exemplu

Vom determina, folosind Algoritmul lui Kruskal, arborele parțial de cost minim pentru graful de mai jos:

Muchiile se vor analiza în ordinea următoare:

1.		Se adaugă muchia (7,8) de cost 1
2.		Se adaugă muchia (3,9) de cost 2
3.		Se adaugă muchia (6,7) de cost 2
4.		Se adaugă muchia (1,2) de cost 4
5.		Se adaugă muchia (3,6) de cost 1
6.		Se ignoră muchia (7,9) de cost 6
7.		Se adaugă muchia (3,4) de cost 7
8.		Se ignoră muchia (8,9) de cost 7
9.		Se adaugă muchia (1,8) de cost 8
10.		Se ignoră muchia (2,3) de cost 8
11.		Se adaugă muchia (4,5) de cost 9
12.		Se ignoră muchia (5,6) de cost 10
13.		Se ignoră muchia (2,8) de cost 11
14.		Se ignoră muchia (4,6) de cost 14

Secvență C++

Următoarea secvență determină costul total al APM-ului, folosind algoritmul lui Kruskal. Presupunem că graful are cel mult 100 de noduri.

struct muchie{
	int i,j,cost;
};

int n , m , t[101];

muchie x[5000];

int main()
{
    cin >> n >> m;

    for(int i = 0 ; i < m ; ++i)
		cin >> x[i].i >> x[i].j >> x[i].cost;

	//sortare tablou x[] după campul cost
    // ... de completat

    //initializare reprezentanti
	for(int i =1 ; i <= n ; ++i)
		t[i] = i;
      //determinare APM
	int S = 0;
	for(int i = 0 ; i < m ; i ++)
		if(t[x[i].i] != t[x[i].j]) // extremitatile fac parte din subrabori diferiti
		{
			S += x[i].cost;
            //reunim subarborii
			int ai = t[x[i].i], aj = t[x[i].j];
			for(int j =1 ; j <= n ; ++j)
				if(t[j] == aj)
					t[j] = ai;
		}
	cout << S << "\n";
	return 0;
}

Vezi și

• Algoritmul lui Prim

Un graf orientat G=(V,E) este tare conex dacă pentru orice pereche de noduri distincte (x,y) există cel puțin un drum de la x la y și există cel puțin un drum de la y la x.

Pentru un graf orientat, se numește componentă tare conexă un subgraf tare conex maximal – prin adăugarea a încă unui nod, subgraful obținut nu mai este tare conex.

Exemplu

Graful de mai sus nu este tare conex. El are trei componente tare conexe.

Verificarea tare conexității. Determinarea componentelor tare conexe

Verificare tare conexității unui graf orientat poate fi privită ca un caz particular al determinării componentelor tare conexe, deoarece, dacă graful are o singură componentă tare conexă atunci el este tare conex. În continuare vom vedea două metode de determinare a componentelor tare conexe. Ambele folosesc noțiunea de graf transpus, pe care o definim în continuare:

Definiție: Fie G=(V,E) un graf orientat. Se numește graf transpus al lui G graful orientat GT=(V,ET), cu aceeași mulțimea a nodurilor și pentru orice pereche de noduri are loc: (x,y) este arc în G dacă și numai dacă (y,x) este arc în GT.

Exemplu

Graf orientat inițial	Graful orientat transpus

Să observăm că pentru două noduri oarecare x, y:

• existența unui drum de la x la y poate fi determinată cu o parcurgere (de exemplu în adâncime) în graful G, pornind din nodul x;
• existența unui drum de la y la x poate fi determinată cu o parcurgere în graful GT, pornind tot din nodul x.

Algoritmul Plus-Minus

Folosind observații de mai sus, pentru a determina componentele tare conexe folosim următorul algoritm, numit Plus-Minus:

• pentru fiecare nod x al grafului care încă nu a fost plasat într-o componentă tare conexă:
  • determinăm toate nodurile în care se poate ajunge din x, folosind graful G și le marcăm într-un tablou cu plus;
  • determinăm toate nodurile din care se poate ajunge în x, folosind graful GT și le marcăm într-un tablou cu minus;
  • nodurile marcate atât cu plus, cât și cu minus, împreună cu x formează o componentă tare conexă;

Exemplu:

Fie graful de mai sus. Să determinăm componenta tare conexă din care face parte nodul 6:

Graful inițial	Graful transpus
S-au marcat cu plus nodurile: 5 7 8	S-au marcat cu minus nodurile: 1 2 3 4 5 7 8

Nodurile marcate de două ori, 5 7 8, împreună cu nodul inițial, 6, formează o componentă tare conexă.

Secvență C++:

• n, a[][] – numărul de noduri și matricea de adiacență
• nrc – numărul de componente tare conexe
• ctc[] – tablou pentru memorarea componentelor tare conexe: ctc[i] = numărul de ordine al componentei din care face parte nodul i
• s[], p[] – tablouri pentru marcarea nodurilor vizitate în timpul parcurgerilor
• să observăm că graful inițial și cel transpus pot fi memorate prin aceeași matrice de adiacență

void df1(int x)
{
    s[x] = 1;
    for(int i =1 ; i <= n ; i ++)
        if(s[i] == 0 && a[x][i] == 1)
            df1(i);
}

void df2(int x)
{
    p[x] = 1;
    for(int i =1 ; i <= n ; i ++)
        if(p[i] == 0 && a[i][x] == 1)
            df2(i);
}

int main()
{
    .....
    for(int i = 1 ; i <= n ; ++i)
        if(ctc[i] == 0)
        {
            for(int j = 1; j <= n ; ++j)
                s[j] = p[j] = 0;
            nrc ++;
            df1(i); df2(i);
            for(int j = 1; j <= n ; ++j)
                if(s[j] == 1 && p[j] == 1)
                    ctc[j] = nrc;
        }
    ....
}

Algoritmul lui Kosaraju

Alt algoritm, mai eficient, pentru determinarea componentelor tare conexe este Algoritmul lui Kosaraju.

Să ne amintim că la parcurgerea în adâncime se pot asocia nodurilor două momente de timp:

• d[x] – momentul când nodul x este descoperit și adăugat pe stivă: timpul de descoperire a nodului
• f[x] – momentul când se termină de vizitat succesorii lui x, iar nodul x se elimină de pe stivă: timpul de finalizare a nodului

Aceste momente de timp vor fi numere naturale între 1 și 2*n, unde n este numărul de noduri din graf.

Algoritmul lui Kosaraju este:

• determinăm graful transpus GT
• parcurgem în adâncime graful și determinăm pentru fiecare nod x timpul de finalizare f[x]
• parcurgem în adâncime graful transpus GT, dar considerăm nodurile în ordinea descrescătoarea timpilor de finalizare
• nodurile din arborii de parcurgere obținuți reprezintă câte o componentă tare conexă

Exemplu:

Graf orientat inițial	Graful orientat transpus

În urma parcurgerii în adâncime a grafului inițial G nodurile în ordinea finalizării sunt:

Parcurgem graful transpus GT analizând nodurile în ordinea inversă a timpilor de finalizare:

• începem cu nodul 1; se vizitează nodurile 3 4; se determină componenta tare conexă {1,3,4};
• continuăm cu nodul 2 (nodurile 1, 3 și 4 au fost vizitate mai devreme); nu se vizitează alte noduri; se determină componenta tare conexă {2};
• continuăm cu nodul 5; se vizitează nodurile 6 8 7; se determină componenta tare conexă {5, 6, 7, 8}.

Secvență C++:

#include <iostream>
#include <fstream>
#include <vector>

using namespace std;

vector<vector<int> > G, GT;

int n , m , contor , nrs;

vector<bool> V;
vector<int> S;

void read()
{
    cin >> n >> m;
    G = GT = vector<vector<int>>(n + 1);
    for(int i = 1 ; i <= m ; i++)
    {
        int a , b;
        cin >> a >> b;
        G[a].push_back(b);
        GT[b].push_back(a);
    }

}

void dfs(int k)
{
    V[k] = true;
    for(auto x : G[k])
        if(!V[x]) 
            dfs(x);
    S.push_back(k);
}

void dfsGT(int k)
{
    V[k]=1;
    for(auto x: GT[k])
        if(! V[x])
            dfsGT(x);

}

int main()
{
    read();

    V = vector<bool> (n + 1, false);
    for(int i = 1 ; i <= n ; i ++)
        if(! V[i]) 
            dfs(i);

    V = vector<bool> (n + 1, false);
    for(vector<int>::reverse_iterator it = S.rbegin() ; it != S.rend() ; it ++)
        if(!V[*it]) {
                contor ++;
                dfsGT(*it);
        }

    cout<<contor;
    return 0;
}

Complexitatea acestui algoritm este aceea a parcurgerii în adâncime: O(n2) dacă memorăm graful prin matricea de adiacență, O(n+m) dacă memorăm graful prin liste de adiacență.

Fie G=(V,E) un graf neorientat conex:

• un nod al grafului se numește punct de articulație sau nod critic dacă subgraful obținut prin eliminarea lui nu este conex;
• o muchie se numește punte sau muchie critică dacă graful parțial obținut prin eliminarea ei nu este conex;
• un graf neorientat se numește biconex dacă nu conține puncte de articulație;
• se numește componentă biconexă un subgraf biconex maximal – prin adăugarea încă unui nod nu mai este biconex.

Exemplu:

Graful inițial	Puncte de articulație	Punți	Componente biconexe

Câteva observații:

• pentru fiecare muchie critică, cel puțin o extremitate este punct de articulație;
• fiecare punct de articulație face parte din cel puțin două componente biconexe;
• nodurile care fac parte dintr-un ciclu aparțin aceleiași componente biconexe;
• fiecare muchie critică reprezintă ea însăși o componentă biconexă;
• o muchie este critică dacă nu face parte dintr-un ciclu;

Pentru a determina punctele de articulație și punțile se poate folosi un algoritm naiv, bazat pe eliminarea succesivă a câte unui nod (muchie) și verificarea conexității. Complexitatea acestor algoritmi este O(n*C), respectiv O(m*C), unde O(C) este complexitatea algoritmului de verificarea a conexității (O(n*n) dacă reprezentăm graful prin matrice de adiacență, O(n+m) dacă reprezentăm graful prin liste de adiacențe).

În cele ce urmează vom prezentat un algoritm bazat pe parcurgerea în adâncime a grafului. Complexitatea sa este aceeași cu a parcurgerii în adâncime.

Considerăm G=(V,E) graful dat și A arborele de parcurgere în adâncime. Reamintim că muchiile graful pot fi doar:

• muchii de parcurgere, folosite la înaintarea în arbore
• muchii de întoarcere; o muchie (k,x) este de întoarcere dacă x este ascendent al lui k în arborele A – nodul x a fost descoperit anterior nodului k

Pentru graful de mai sus, arborele de parcurgere este următorul – muchiile de parcurgere sunt desenate cu linii continue, cele de întoarcere cu linii întrerupte.

Observăm următoarele:

• un nod k al grafului, diferit de rădăcina arborelui DFS, este punct de articulație dacă și numai dacă are un descendent direct x în arborele A cu proprietatea că de la niciun descendent al lui x sau de la x nu există muchie de întoarcere la niciun ascendent al lui k;
• rădăcina arborelui DFS este punct de articulație dacă și numai dacă are în acest arbore cel puțin doi descendenți direcți.

Pentru a determina punctele de articulație, punțile și componentele biconexe vom determina pentru fiecare nod k următoarele informații:

• nivel[k] – nivelul pe care se află nodul k în arborele DFS;
  • nivel[rădăcină] = 1;
  • nivel[k] = nivel[tata[k]] + 1;
• nma[k] – nivelul minim la care se poate ajunge din k, mergând numai pe muchii de arbore și folosind ca ultimă muchie o muchie de întoarcere. Îl vom numi nivelul minim accesibil și este egal cu minimul dintre următoarele 3 valori :
  • nivelul nodului curent
  • minimul dintre nivelurile nodurilor cu care este legat nodul curent printr-o muchie de întoarcere
  • minimul dintre nivelurile minime accesibile ale fiilor nodului curent din cadrul arborelui DFS

Pentru graful de mai sus aceste valori sunt următoarele:

Cu ajutorul acestor valori, un nod k care nu este rădăcina arborelui este punct de articulație dacă și numai dacă are cel puțin un fiu x pentru care nivelul minim accesibil este mai mare sau egal cu nivelul nodului (nivel[k] <= nma[x]). Să analizăm nodurile:

• 1 nu este punct de articulație, deoarece este rădăcina arborelui și are un singur descendent direct
• 2 este punct de articulație, deoarece 3 este fiu al lui 2 și nivel[2] <= nma[3]
• 3 nu este punct de articulație, deoarece nu are niciun fiu
• 4 nu este punct de articulație, deoarece nu are niciun fiu
• 5 este punct de articulație deoarece 7 este fiu al lui 5 și nivel[5] <= nma[7]
• 6 nu este punct de articulație; pentru singurul fiu al lui 6, 8 relația este nivel[6] > nma[8]
• 7 este punct de articulație deoarece 6 este fiu al lui 7 și nivel[7] <= nma[6]
• 8 nu este punct de articulație deoarece nu are fii

Fie (k,x) o muchie de arbore, în care k este tatăl lui x. Această muchie este critică dacă și numai dacă (nivel[k] < nma[x]). Muchiile de întoarcere nu sunt niciodată muchii critice, deoarece aparțin întotdeauna unor cicluri.

Cele două șiruri de valori se construiesc în timpul parcurgerii DFS. Fie k nodul curent în parcurgerea DFS:

• stabilim nivel[k] = nivel[tata[k]] + 1 – această valoare va rămâne neschimbată până la final;
• inițializăm nma[k] = nivel[k]
• parcurgem nodurile adiacente cu k. Fie x un asemenea nod:
  • dacă x a fost deja parcurs și nu este tatăl lui k, muchia (k,x) este muchie de întoarcere. Dacă este cazul actualizăm nma[k] la valoarea nivel[x] (dacă nivel[x] este mai mic decât valoarea actuală a lui nma[k]);
  • dacă x nu a fost încă parcurs, continuăm parcurgerea din x – îl adăugăm pe stivă/apel recursiv. La eliminarea de pe stivă/ revenirea din autoapel, actualizăm valoarea nma[k] la valoarea nma[x] (dacă nma[k] este mai mare decât nma[x], acesta din urmă este calculat deja)

Următorul pseudocod descrie cum se calculează pentru fiecare nod al grafului nivelul și nivelul minim accesibil, folosind parcurgerea în adâncime:

subprogram DFS(k, tata)
    V[k] ← true
    nivel[k] ← nivel[tata] + 1
    nma[k] ← nivel[k]
    pentru x - nod adiacent cu k
        dacă x ≠ tata
            dacă V[x] = true atunci
                dacă nma[k] > nivel[x] atunci
                    nma[k] ← nivel[x]
                sf_dacă
            altfel
                DFS(x,k)
                dacă nma[k] > nma[x] atunci
                    nma[k] ← nma[x]
                sf_dacă

                // determinare puncte de articulație

                // determinare punți

                // determinare componente biconexe

            sf_dacă
        sf_dacă
    sf_pentru
sf_subprogram

Pentru a determina punctele de articulație:

• la eliminarea de pe stivă a nodului x (revenirea din autoapel) verificăm dacă acest și nodul părinte k verifică relația nivel[k] <= nma[x]; în caz afirmativ, decidem că nodul k este critic;
• pentru a stabili dacă rădăcina este punct de articulație trebuie să-i numărăm descendenții direcți în arbore.
• Observație: un punct de articulație poate fi descoperit de mai multe ori – dacă există mai mulți fii ai săi care respectă relația de mai sus.

//determinare puncte de articulație
dacă nivel[k] ≤ nma[x] și nod ≠ rădăcină atunci
    //nodul k este punct de articulație
sf_dacă

Pentru a determina punțile:

• la eliminare de pe stivă a nodului x/revenirea din autoapel vom determina muchiile de parcurgere (k,x) pentru care nivelul lui k este mai mic decât nivelul minim accesibil al lui x: nivel[k] < nma[x].

//determinare punți
dacă nivel[k] < nma[x] atunci
    //muchia (k,x) este punte
sf_dacă

Pentru a determina componentele biconexe:

• utilizăm o stivă suplimentară S, pe care adaugăm noduri la vizitarea lor conform parcurgerii și le eliminăm la determinarea unei componente biconexe;
  • ordinea nodurilor din stiva S este cea a parcurgerii în adâncime;
• dacă pentru nodul curent k avem un descendent direct x pentru care nivel[k] <= nma[x], vom elimina de pe stivă nodurile până la nodul x, inclusiv acesta;
  • nodurile eliminate, împreună cu nodul k reprezintă o componentă biconexă;
  • eliminarea se face până la x, nu până la k, deoarece între acestea, pe stivă, pot fi noduri din altă componentă biconexă.
• Observație: condiția nivel[k] <= nma[x] are loc întotdeauna pentru rădăcina arborelui DFS, chiar dacă acesta nu este punct de articulație. În acest caz se determină o componentă biconexă din care face rădăcina. Acest lucru se întâmplă și când graful dat este biconex: determinarea componentei biconexe se face la revenirea în rădăcină.

...
V[k] ← true
Adaugă(S,k)
....
//determinare componente biconexe
dacă nivel[x] ≤ nma[k] atunci
    câttimp Vârf(S) ≠ x execută
        Vârf(S) se adugă la componenta curentă
        Elimină(S)
    sf_câttimp
    x se adaugă la componenta curentă
    Elimină(S)
    k se adaugă la componenta curentă
sf_dacă

În jurul anului 1960 a fost descoperit un algoritm pentru drumuri în grafuri orientate. Descoperirea a fost făcută independent de către trei oameni de stiință în domeniul algoritmilor: Robert Floyd, Bernard Roy și Stephen Warshall.

Algoritmul se regăsește sub diferite denumiri care conțin numele descoperitorilor, este bazat pe programarea dinamică și poate fi utilizat în următoarele două moduri:

• pentru un graf orientat oarecare determină matricea drumurilor – stabilește despre oricare două noduri x y dacă există drum de la x la y – este de regulă cunoscut sub numele Roy-Warshal
• pentru un graf orientat ponderat (cu costuri) – determină pentru fiecare pereche de noduri costul minim al unui drum cu extremitățile în acele noduri – este de regulă cunoscut sub numele Roy-Floyd

Ambele variante permit și reconstituirea unor drumuri între două noduri date.

În 1736, matematicianul elvețian Leonard Euler a rezolvat o problemă cunoscută astăzi ca “Problema celor șapte poduri din Königsberg”. Prin orașul Königsberg, azi Kaliningrad trece un râu pe care sunt două insule, acestea și malurile fiind unite prin poduri ca în imaginea de mai jos.

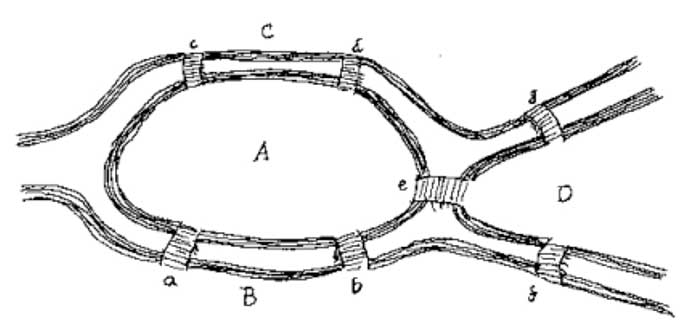
Leonard Euler a demonstrat că nu este posibil ca o persoană să traverseze fiecare pod o singură dată. În onoarea sa, o categorie specială de grafuri se numesc grafuri euleriene.

Definiții:

• Într-un graf neorientat, se numește lanț eulerian un lanț simplu în care apare fiecare muchie (fiind lanț simplu, fiecare muchie apare o singură dată).
• Într-un graf neorientat, se numește ciclu eulerian un ciclu în care apare fiecare muchie.
• Un graf neorientat se numește graf eulerian dacă conține un ciclu eulerian.

Exemplu:

În graful de mai sus ciclul (1 2 4 5 3 6 5 2 3 1) este eulerian.

Teoremă:

Un graf neorientat fără vârfuri izolate este eulerian dacă și numai dacă este conex și toate vârfurile au grad par.
Un graf neorientat fără vârfuri izolate conține un lanț eulerian, dacă și numai dacă este conex și toate vârfurile au grad par, mai puțin două. Aceste vârfuri vor fi extremitățile lanțului eulerian.

Pentru determinarea unui ciclu eulerian se pot folosi mai mulți algoritmi. Unul dintre aceștia este asemănător cu parcurgerea în adâncime. Vom folosi o stivă (eventual memoria STACK prin intermediul recursivității):

• adăugăm pe stivă un vârf oarecare – de exemplu 1;
• cât timp stiva nu este vidă
  • fie k – nodul din vârful stivei
  • determinăm nodurile x adiacente cu k. Eliminăm muchia [k,x] și adăugăm nodul x pe stivă (apel recursiv)
    • continuăm cu nodul situat în vârful stivei
  • adăugăm nodul k într-o listă
  • eliminăm nodul k din stivă
• lista construită reprezintă ciclu eulerian

Important:

• la vizitarea unui vârf, acesta nu va fi marcat, pentru a permite revenirea în el;
• finitudinea algoritmului este asigurată de faptul că muchiile se elimină din graf;

Secvență C++:

Considerăm un graf cu n vârfuri, memorat prin intermediul matricei de adiacență, A[][]. Tabloul L[] reprezintă lista în care se memorează ciclul eulerian. Toate variabilele sunt globale:

void Euler(int k)
{
	for(int i = 1 ; i <= n ; i ++)
		if(A[k][i] == 1)
		{
			A[k][i] = A[i][k] = 0;
			Euler(i);
		}
	L[++p] = k;
}
...
Euler(1);
...

Algoritmul de mai sus poate fi utilizat și pentru determinarea unui lanț eulerian. Parcurgerea trebuie să înceapă însă din unul dintre vârfurile cu grad impar.

Problema comis voiajorului este o problemă celebră de informatică: Un comis-voiajor (agent comercial) trebuie să viziteze n orașe. Cunoscându-se șoselele existente între orașe, să se determine o modalitate (toate modalitățile) prin care comis-voiajorul poate parcurge fiecare oraș o singură dată și se întoarce în orașul de plecare.

Dacă asociem problemei un graf neorientat, constatăm că trebuie să determinăm un ciclu elementar (toate ciclurile elementare) care trece prin toate vârfurile grafului. Un astfel de ciclu se numește ciclu hamiltonian.

Definiții:

• Într-un graf neorientat, se numește lanț hamiltonian un lanț elementar care conține toate vârfurile grafului.
• Într-un graf neorientat, se numește ciclu hamiltonian un ciclu elementar care conține toate vârfurile grafului.
• Un graf neorientat se numește graf hamiltonian dacă conține un ciclu hamiltonian.

Pentru un graf orientat se pot definii noțiuni similare, de drum hamiltonian și circuit hamiltonian

Exemplu:

În graful de mai sus sunt evidențiate muchiile care fac parte dintr-un ciclu hamiltonian: (1, 2, 5, 4, 6, 3).

În anumite condiții se poate stabili că un graf dat este hamiltonian. Dar aceste condiții sunt “de suficiență”. Dacă nu sunt îndeplinite, nu înseamnă că graful nu este hamiltonian!

Teoreme:

• Fie G=(X,U) un graf neorientat cu \( n \) vârfuri și un lanț hamiltonian \( v_1, v_2, \cdots, v_n \). Dacă \( d(v_1) + d(v_n) \geq n\), atunci graful este hamiltonian, unde \( d(x) \) este gradul vârfului \(x \).
• Fie G=(X,U) un graf neorientat cu \( n \) vârfuri. Dacă pentru orice pereche de vârfuri neadiacente distincte \( v_i, v_j \) avem relația \( d(v_i) + d(v_j) \geq n\), atunci graful este hamiltonian.
• Un graf neorientat în care gradul fiecărui vârf este mai mare sau egal cu jumătate din numărul de vârfuri este hamiltonian.
• Un graf complet cu \(n > 2\) vârfuri conține \(\frac{(n-1)!}{2}\) cicluri hamiltoniene.

Considerăm un graf neorientat ponderat (cu costuri) conex G. Se numește arbore parțial un graf parțial al lui G care este arbore. Se numește arbore parțial de cost minim un arbore parțial pentru care suma costurilor muchiilor este minimă.

Dacă graful nu este conex, vorbim despre o pădure parțială de cost minim.

Algoritmul lui Prim permite determinarea unui arbore parțial de cost minim (APM) într-un graf ponderat cu N noduri.

Descrierea algoritmului

Determinarea APM-ului se face astfel:

• se stabilește un nod de plecare; acesta va fi rădăcina arborelui, care se va crea pas cu pas, prin adăugarea de noi noduri;
• în mod repetat:
  • se alege un nod neadăugat încă în arborele curent pentru care muchia dintre el și un nod din arbore are cost minim;
  • se adăugă nodul în arbore;
• când nu se mai poate face alegerea unui asemenea nod, fie au fost adăugate toate nodurile, fie graful nu este conex și au fost adăugate în arbore toate nodurile din componenta conexă a nodul inițial;
• dacă graful nu este conex, continuăm cu următoarea componentă conexă.

Observație: arborele parțial de cost minim al unui graf neorientat nu este unic, însă toate APM-urile vor avea același cost.

Exemplu

Mai jos este descris modul în care se aleg nodurile care se adaugă în arbore pentru un graf ponderat cu N=9 noduri:

Algoritmul poate fi implementat în mai multe moduri, cu complexități diferite.

Varianta \(N^3\)

• în mod repetat (de cel mult N-1 ori):
  • se aleg două noduri adiacente, un nod din arbore și un nod din afara acestuia, astfel încât muchia determinată de cele două noduri să aibă costul minim
  • nodul ales din afara arborelui curent se va adăuga în arbore

Varianta \(N^2\)

Față de varianta anterioară se evită căutarea propriu zisă a nodului din arbore, căutându-se efectiv numai nodul din afara acestuia. Pentru aceasta se păstrează un șir d[] cu următoarea semnificație: pentru un nod k încă neadăugat în arbore, d[k] reprezintă costul minim al unei muchii având o extremitate k și o extremitate în arbore; dacă o asemenea muchie nu există d[k] = INFINIT.

Dacă determinarea succesivă a nodurilor din afara arborelui se face prin parcurgerea șirului d[], complexitatea devine O(N2).

Varianta \(N \log N\)

Se poate evita parcurgerea șirului d[] prin memorarea nodurilor din arbore într-o structură de date de tip heap, în vârful heap-ului fiind nodul k pentru care d[k] are valoare minimă. În acest fel complexitatea algoritmului devine O(N logN).

Vezi și

• Algoritmul lui Kruskal

Grafurile au numeroase aplicații în diverse domenii: proiectarea circuitelor electrice, determinarea celui mai scurt drum dintre două localități, rețelele sociale (ex. Facebook), etc.

Primele rezultate legate de teoria grafurilor au fost obținute de matematicianul Leonard Euler, cel care a studiat Problema podurilor din Königsberg, din imaginea de mai jos. A demonstrat că problema nu are soluție, iar în onoarea lui o categorie specială de grafuri au fost numite grafuri euleriene.

Terminologie

Definiție: Se numește graf neorientat o pereche ordonată de mulțimi G=(X,U), unde:

• X este o mulțime finită și nevidă de elemente numite vârfuri sau noduri;
• U este o mulțime finită de submulțimi cu două elemente din X, numite muchii.

Vom nota în continuare vârfurile cu valori între 1 și n – unde n este număru de vârfuri din graf, iar muchiile cu [x,y] sau (x,y), unde x și y sunt vârfuri și se numesc extremitățile muchiei.

Un vecin al unui vârf x este orice vârf y cu proprietatea că există muchia [x,y].

Două vârfuri între care există muchie se numesc adiacente.

Două muchii sunt incidente dacă au o o extremitate comună. Un vârf este incident cu o muchie dacă vârful este extremitate a acelei muchii.

Mulțimea muchiilor are proprietatea de simetrie: dacă [x,y] este muchie, atunci și [y,x] este muchie.

Conform definiției:

• într-un graf neorientat nu există muchie de la un vârf la el însuși;
• intre două vârfuri distincte există cel mult o muchie.

Exemplu: Fie G=(X,U), unde:

• X={1,2,3,4,5,6,7,8,9,10,11}
• U={[1,4],[1,5],[2,3],[2,8],[3,11],[4,5],[4,9],[7,10],[8,11]}

Gradul unui vârf

Definiție Într-un graf neorientat se numește grad al unui vârf numărul de vârful adiacente cu acesta (sau numărul de muchii incidente cu acesta). Gradul unui vărf x se notează d(x) (degree).

Observații:

• un vârf cu gradul 0 se numește izolat. În graful de mai sus, vârful 6 este izolat.
• un vârf cu gradul 1 se numește terminal. În graful de mai sus, vârful 9 este vârf terminal.
• gradul maxim al unui vârf într-un graf cu n vârfuri este n-1.

Teoremă: Într-un graf neorientat, suma gradelor tuturor vârfurilor este dublul numărului de muchii.

Consecințe:

• Suma gradelor tuturor vârfurilor este număr par.
• Într-un graf neorientat, numărul de vârfuri de grad impar este întotdeauna par.

Întrebare: Este posibil ca într-un grup de 5 persoane, fiecare persoană să aibă exact 3 prieteni?

Reprezentarea grafurilor neorientate

Matricea de adiacență

Pentru un graf neorientat G=(X,U) cu n vârfuri, matricea de adiacență este o matrice cu n linii și n coloane și elemente din {0,1}, cu: \( A_{i,j} = \left\{ \begin{array}{ll} 1 & \mbox{dacă } [i,j] \in U \\ 0 & \mbox{dacă } [i,j] \notin U \end{array} \right. \)

Exemplu: Pentru graful neorientat de mai jos avem următoarea matrice de adiacență:

\( A = \left( \begin{array}{ccccc} 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 \end{array} \right) \)

Observații:

• matricea de adiacență este simetrică față de diagonala principală;
• elementele de pe diagonala principală sunt 0;
• gradul unui vârf x este egal cu numărul de elemente 1 de pe linia (sau coloana) x;
• suma tuturor elementelor din matricea de adiacență a unui graf neorientat este egală cu dublul numărului de muchii din graf.

Lista de muchii

Lista de muchii a unui graf neorientat reprezintă o mulțime ce conține toate muchiile din graf.

Pentru graful alăturat, lista de muchii este:

\( U = \left\{ [1,2],[1,5],[2,5],[4,5] \right\} \)

Pentru reprezentarea în memorie putem folosi:

• un tablou unidimensional cu elemente de tip struct {int I,J;}
• două tablouri unidimensionale cu elemente de tip int
• o listă alocată dinamic
• etc.

Liste de adiacențe (de vecini)

Pentru un graf neorientat cu G=(X,U) se va memora numărul de vârfuri n și apoi, pentru fiecare vârf x, lista vârfurilor adiacente cu x, adică a vârfurilor y cu proprietatea că există muchia [x,y].

Pentru graful alăturat, listele de adiacență sunt:

1: 2 5
2: 1 5
3: vidă
4: 5
5: 1 2 4

La reprezentarea în memorie trebuie avut în vedere că dimensiunile listelor de vecini sunt variabile. De aceea, este neeficientă utilizarea unor tablouri alocate static. Astfel, putem folosi:

• un șir de n tablouri unidimensionale alocate dinamic;
• un șir de n vectori din STL;
• un șir de n liste simplu (dublu) înlănțuite alocate dinamic.

Graf parțial. Subgraf. Graf complementar

Definiție. Fie G=(X, U) un graf neorientat. Se numeşte graf parțial al grafului G, graful neorientat G1=(X, U1), unde U1 ⊆ U.

Din definiție rezultă:

• Un graf parțial al unui graf neorientat G=(V,U), are aceeaşi mulțime de vârfuri ca şi G, iar mulțimea muchiilor este o submulțime a lui U sau chiar U.
• Fie G=(X, U) un graf neorientat. Un graf parțial al grafului G se obține păstrând vârfurile şi
  eliminând eventual nişte muchii (se pot elimina şi toate muchiile sau chiar nici una).

Definiție. Fie G=(X, U) un graf orientat. Se numeşte subgraf al grafului G graful neorientat G1=(X1,U1) unde X1 ⊆ X iar U1 conține toate arcele din U care au extremitățile în X1.

Din definiție rezultă:

• Fie G=(X,U) un graf orientat. Un subgraf al grafului G, se obține ştergând eventual anumite
  vârfuri şi odată cu acestea şi muchiile care le admit ca extremitate (nu se pot şterge toate vârfurile deoarece s-ar obține un graf cu mulțimea vârfurilor vidă).

Definiție. Fie G=(X, U) un graf neorientat. Se numeşte graf complementar al grafului G, graful neorientat G1=(X, U1), cu proprietatea că două vârfuri x și y sunt adiacente în G1 dacă și numai dacă nu sunt adiacente în G.

Exemplu:

Graful inițial	Graf parțial	Subgraf	Graf complementar
	S-au eliminat muchiile [1,2], [3,1]	S-a eliminat vârfurile 3 5 și toate muchiile incidente cu ele.	O muchie [x,y] apare în graful complementar dacă și numai dacă nu apare în graful inițial.

Observații. Un graf neorientat oarecare poate avea mai multe grafuri parțiale și subgrafuri, dar un unic graf complementar. Mai precis:

Teoremă: Fie G un graf neorientat cu n vârfuri și m muchii. Atunci:

• graful G admite \( 2 ^ m \) grafuri parțiale;
• graful G admite \( 2 ^ n – 1 \) subgrafuri;
• graful G admite un unic graf complementar.

Justificare:

Să ne amintim că o mulțime cu a elemente are \( 2 ^ a \) submulțimi, inclusiv mulțimea vidă și mulțimea inițială. Atunci:

• orice submulțime a mulțimii muchiilor induce un graf parțial. Sunt m muchii, deci \( 2 ^ m \) submulțimi, deci \( 2 ^ m \) grafuri parțiale.
• orice submulțime a mulțimii vârfuri induce un subgraf, mai puțin mulțimea vidă – un graf nu poate avea 0 vârfuri. Similar ca mai sus, sunt \( 2^n – 1 \) subgrafuri.
• graful complementar este unic determinat, deoarece complementara unei submulțimi față de o mulțime dată este unic determinată.

Graf nul. Graf complet. Graf regulat. Graf bipartit

Definiție: Un graf neorientat se numește graf nul dacă mulțimea muchiilor este vidă.

Într-un graf nul toate vârfurile sunt izolate.

Definiție. Fie G=(X, U) un graf neorientat. Graful G se numește graf complet dacă oricare două vârfuri
distincte ale sale sunt adiacente. Un graf complet cu n vârfuri se notează Kn.

Exemplu: Graful următor este graful K5.

Într-un graf complet cu n vârfuri sunt \( C_n ^2 = { {n*(n-1)} \over 2 } \) muchii și fiecare vârf are gradul n-1.

Propoziție: Sunt \( 2 ^ {{n*(n-1)} \over 2} \) grafuri neorientate distincte cu n vârfuri.

Definiție: Un graf în care toate nodurile au acelaşi grad se numește graf regulat.

Exemplu: Graful de mai jos este regulat.

Definiţie: Un graf G=(X, U) se numește graf bipartit dacă există două mulţimi nevide A și B astfel încât X=A ∪ B, A ∩ B = ∅ şi orice muchie u a lui G are o extremitate în A iar cealaltă în B. Mulţimile A şi B formează o partiţie a lui X.

Exemplu: Graful următor este bipartit. A={1,2,5,7} și B={3,4,6}.

Definiție: Un graf bipartit G=(X,U) se numește bipartit complet dacă pentru oricare două vârfuri \( x \in A\) și \( y \in B \), există în graf muchia [x,y]; adică \( [x,y] \in U \).

Exemplu: Graful următor este bipartit complet.

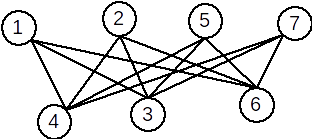
Conexitate

Lanț, ciclu

Definiție: Se numește lanț o succesiune de vârfuri \( L = \left[ x_1, x_2, \cdots x_k \right] \) cu proprietatea că oricare două vârfuri consecutive sunt adiacente.

Vârfurile x1 şi xk se numesc extremitățile lanțului. Numărul k-1 se numește lungimea lanțului și este numărul de muchii din care este format.

Lanțul care conține numai vârfuri distincte, două câte două, este lanț elementar.

Lanțul care conține numai muchii distincte este lanț simplu. Dacă muchiile unui lanț nu sunt distincte se numește lanț compus.

Definiție: Se numește ciclu un lanț simplu în care primul vârf este identic cu ultimul. Dacă toate vârfurile sunt distincte, mai puțin primul și ultimul, se numește ciclu elementar.

Lungimea unui ciclu este egală cu numărul de muchii din ciclu. Lungimea minimă a unui ciclu este 3.

Un ciclu se numește par dacă lungimea sa este pară, respectiv impar în caz contrar.

Un graf neorientat care nu conține niciun ciclu se numește aciclic.

Exemple: În graful de mai jos:

• \( [2,4,1,3,5,7] \) este un lanț elementar
• \( [3,5,7,6,5,1] \) este un lanț neelementar, dar simplu
• \( [2,3,5,7,6,5,3,1] \) este un lanț compus
• \( [1,5,3,2,4,1] \) este un ciclu elementar
• \( [1,3,5,7,6,5,1] \) este un ciclu neelementar

Graf conex. Componente conexe

Definiție: Un graf neorientat se numește graf conex dacă pentru oricare două vârfuri x și y diferite ale sale, există cel puțin un lanț care le leagă, adică x este extremitatea inițială și y este extremitatea finală.

Un graf cu un singur nod este, prin definiție, conex.

Definiție: Se numește componentă conexă a unui graf G=(X,U) un subgraf H=(Y, V), conex, al lui G
care are proprietatea că nu există nici un lanț în G care să lege un vârf din Y cu un vârf din X – Y.

Subgraful H este conex și maximal cu această proprietate (dacă s-ar mai adăuga un vârf nu ar mai fi conex.)

Un graf este conex dacă admite o singură componentă conexă.

Exemple:

Graful următor este conex:

Graful următor nu este conex și are 4 componente conexe.

Definiție: Un graf este biconex dacă este conex şi pentru orice vârf eliminat subgraful generat îşi păstrează proprietatea de conexitate.

Arbore. Pădure

Definiție: Se numește arbore un graf conex și aciclic.

Exemplu: Graful următor este arbore:

Observații:

• Un arbore cu n vârfuri are n-1 muchii.
• Un arbore este un graf conex și minimal cu această proprietate; dacă s-ar mai elimina o muchie, graful nu ar mai fi conex.
• Un arbore este un graf aciclic și maximal cu această proprietate; dacă s-ar mai adăuga o muchie, s-ar obține un ciclu.

Un graf parțial care este arbore se numește arbore parțial.

Un graf care nu conține cicluri se mai numește pădure. Într-o pădure fiecare componentă conexă este arbore.

Graf hamiltonian. Graf eulerian

Definiție: Se numește graf hamiltonian un graf care conține un ciclu hamiltonian. Se numește ciclu hamiltonian un ciclu elementar care conține toate vârfurile grafului.

Exemplu: Graful următor este hamiltonian. Un ciclu hamiltonian este: \( [1,4,2,3,7,6,5,1] \)

Teoremă: Un G un graf neorientat. Dacă are n≥3 vârfuri şi gradul oricărui vârf verifică inegalitatea d(x)≥n/2 atunci G este hamiltonian.

Definiție: Se numește graf eulerian un graf care conține un ciclu eulerian. Se numește ciclu eulerian un ciclu care conține toate muchiile grafului.

Exemplu: Graful următor este eulerian. Un ciclu eulerian este: \( [1,4,2,1,3,2,7,3,5,7,6,5,1] \)

Teoremă: Un graf G = (X,U), fără vârfuri izolate, este eulerian dacă şi numai dacă este conex şi
gradele tuturor vârfurilor sale sunt numere pare.